[学习笔记] L1-PCA
L1-PCA
Intro
PCA的本质就是从高维空间向低维空间投影,投影的本质又是左乘(或右乘)一个向量(表征原来特征空间到投影后特征空间的权重),经过线性加权,转换到低维空间表征,如果将向量换成矩阵(假设由m个向量组成),则是将原高维空间降维到m维空间上去。
L1-PCA解决的问题是outlier问题(一般PCA假设噪声服从高斯分布,如果有异常不服从,那么此时PCA的效果将非常差),一般PCA是对outlier比较敏感的,而L1-PCA不对outlier敏感.
PCA回顾
有必要从数学角度理解一下PCA。
就像上面我说的,PCA本质是做一种变换,一种变换往往可以通过矩阵乘积来表征,因此:
\[
定义向量a \in R^{p \times 1},特征矩阵X\in R^{n \times p},那么将X降维到1维是相当简单:\\X' = Xa,x'\in R^{n \times 1}
\]
我们学过信号处理我们知道(稍微后面一点),信号往往具有较大的方差,而噪声的方差是较小的,因此我们就很当然的认为,经过降维后的数据应该具有较大的方差。因此,下一步就是方差最大化:
\[
\sigma^2_a = (Xa)^T(Xa) = a^TX^TXa = a^TVa
\]
下面的任务就成了最大化方差优化求解a的问题了,我们引入约束条件
\[
z = a^TVa - \lambda(a^Ta - 1)\\a^Ta = 1\\\frac{\partial z}{\partial a} = (V+V^T)a - 2 \lambda a = 2Va - 2\lambda a = 0 \\ 可以得到\\(V - \lambda I)a = 0
\]
显然a就是V的特征向量,那么后面我们对V进行特征值分解,就拿到这些向量a啦。
还有一个问题,就是保留更多的信息,也就是方差,所以计算每个成分的方差,从大到小排序取合适即可。
L1-PCA
L1-PCA的思想是,经过降维变换之后,新矩阵的L1范数应该足够大,L1范数表征的是所有行绝对值求和最大的列对应的值。
传统的PCA其实还有个等价形式(具体证明请查阅相关资料):
\[
\max_{W^TW=I} ||WX||_2^2
\]
也就是最大化二范数,而L1-PCA就是将L2范数换成了L1范数,这虽然是不等价的,但是却可以在结果上相似,并且L1范数试验下要更加对outlier鲁棒。
因此L1-PCA求解的问题就是
\[
\max_{W^TW=I} ||WX||_1
\]
由于直接求解这个问题是很困难的,所以我们通常通过贪婪法来求,也就是先求一个变换向量w,在求第二个变换向量,以此类推,一个一个求,而不是一次求完一个矩阵。求解一个变换向量w,问题就变成了:
\[
w^* = arg\max_w ||w^TX||_1 = arg \max_w \sum_1^{n}|w^Tx_i|,subject. to. ||w||_2=1
\]
优化过程为(t代表轮次):
\[
w(t+1) = \frac{\sum_{i=1}^{n}p_i(t)x_i}{||\sum_{i=1}^{n}p_i(t)x_i||_2}\\p_i(t)=\left\{\begin{aligned}1 & ,w^T(t)x_i \ge 0 \\-1 & ,w^T(t)x_i <0 \\\end{aligned}\right.
\]
更新训练数据x
\[
x_i^m = x_i^{m-1} - w_{m-1}(w^T_{m-1}x_i^{m-1}),i = 1...n
\]
具体的证明请见:
Coding
很抱歉上一版程序由于我是半夜写的,图最后画错了,今天起来看到了,遂更正了。
'''
@Descripttion: This is Aoru Xue's demo, which is only for reference.
@version:
@Author: Aoru Xue
@Date: 2019-12-12 22:57:47
@LastEditors: Aoru Xue
@LastEditTime: 2019-12-14 00:21:12
'''
import numpy as np
import copy
from matplotlib import pyplot as plt
from numpy import linalg
class L1PCA():
def __init__(self,):
pass
def __call__(self,x,out_n = 2): # x (100,16)
w = np.ones(shape = (x.shape[0],out_n))
X = copy.copy(x)
# 收的得到第一个w
for epoch in range(300):
w_t = w[:,0:1] # (100,1)
top = np.zeros(shape = (X.shape[0],1)) # (100,1)
for i in range(x.shape[1]):
xi = X[:,i:i+1] # (100,1)
pit = 0
if w_t.T.dot(xi)>=0: # (1,100)@(100,1)
pit = 1
else:
pit = -1
top += (pit * xi)
bottom = np.sqrt(np.sum(top**2))
w[:,0:1] = top/bottom
for j in range(1,out_n):
for i in range(X.shape[1]):
b = w[:,j-1:j]*(w[:,j-1:j].T.dot(X[:,i]))
X[:,i:i+1] = X[:,i:i+1] - b
for epoch in range(300):
w_t = w[:,j:j+1] # (100,1)
top = np.zeros(shape = (X.shape[0],1)) # (100,1)
for i in range(X.shape[1]):
xi = X[:,i:i+1] # (100,1)
pit = 0
if w_t.T.dot(xi)>=0: # (1,100)@(100,1)
pit = 1
else:
pit = -1
top += pit * xi
bottom = np.sqrt(np.sum(top**2))
w[:,j:j+1] = top/bottom
return w.T.dot(x)
class PCA():
def __init__(self,):
pass
def __call__(self,x,out_n = 2): #x (100,16)
Ex = np.mean(x,axis = 0).reshape(-1,4).T
Rx = np.cov(x.T)
eigs,D = linalg.eig(Rx) # val(,10) and vec(10,10)
indices = np.argsort(eigs)
U = D[indices[:- out_n - 1:-1],:] # 5个 (5,10)
Y = U.dot((x.T - Ex)) # (5,1000) 霍特林变换(5,1000)
return Y
if __name__ == '__main__':
dataset_path = "/home/xueaoru/下载/iris.data"
dataset = np.loadtxt(dataset_path,dtype = np.str,delimiter=',')
x = dataset[:,:-1].astype(np.float)
y = dataset[:,-1]
yy = list(set(y))
plt.figure(figsize=(12, 8))
plt.subplot(4,2,1)
plt.subplots_adjust(hspace = 1)
plt.title("attr 0 and attr 1")
for c,target in zip("rgb",yy): # y is the label
plt.scatter(x[y == target,0],x[y== target,1],marker = 'x',c = c,label = target)
plt.subplot(4,2,2)
plt.title("attr 0 and attr 2")
for c,target in zip("rgb",yy): # y is the label
plt.scatter(x[y == target,0],x[y== target,2],marker = 'x',c = c,label = target)
plt.subplot(4,2,3)
plt.title("attr 0 and attr 3")
for c,target in zip("rgb",yy): # y is the label
plt.scatter(x[y == target,0],x[y== target,3],marker = 'x',c = c,label = target)
plt.subplot(4,2,4)
plt.title("attr 1 and attr 2")
for c,target in zip("rgb",yy): # y is the label
plt.scatter(x[y == target,1],x[y== target,2],marker = 'x',c = c,label = target)
plt.subplot(4,2,5)
plt.title("attr 1 and attr 3")
for c,target in zip("rgb",yy): # y is the label
plt.scatter(x[y == target,1],x[y== target,3],marker = 'x',c = c,label = target)
plt.subplot(4,2,6)
plt.title("attr 2 and attr 3")
for c,target in zip("rgb",yy): # y is the label
plt.scatter(x[y == target,2],x[y== target,3],marker = 'x',c = c,label = target)
plt.subplot(4,2,7)
plt.title("Normal PCA")
pca = PCA()
#x = pca(x.T).T
x1 = pca(x).T
#print(x.shape)
for c,target in zip("rgb",yy): # y is the label
plt.scatter(x1[y == target,0],x1[y== target,1],marker = 'x',c = c,label = target)
plt.subplot(4,2,8)
plt.title("L1-PCA")
l1pca = L1PCA()
x2 = l1pca(x.T).T
print(x2)
for c,target in zip("rgb",yy): # y is the label
plt.scatter(x2[y == target,0],x2[y== target,1],marker = 'x',c = c,label = target)
plt.show()
#x = np.random.rand(100,16)
#pca(x)可视化
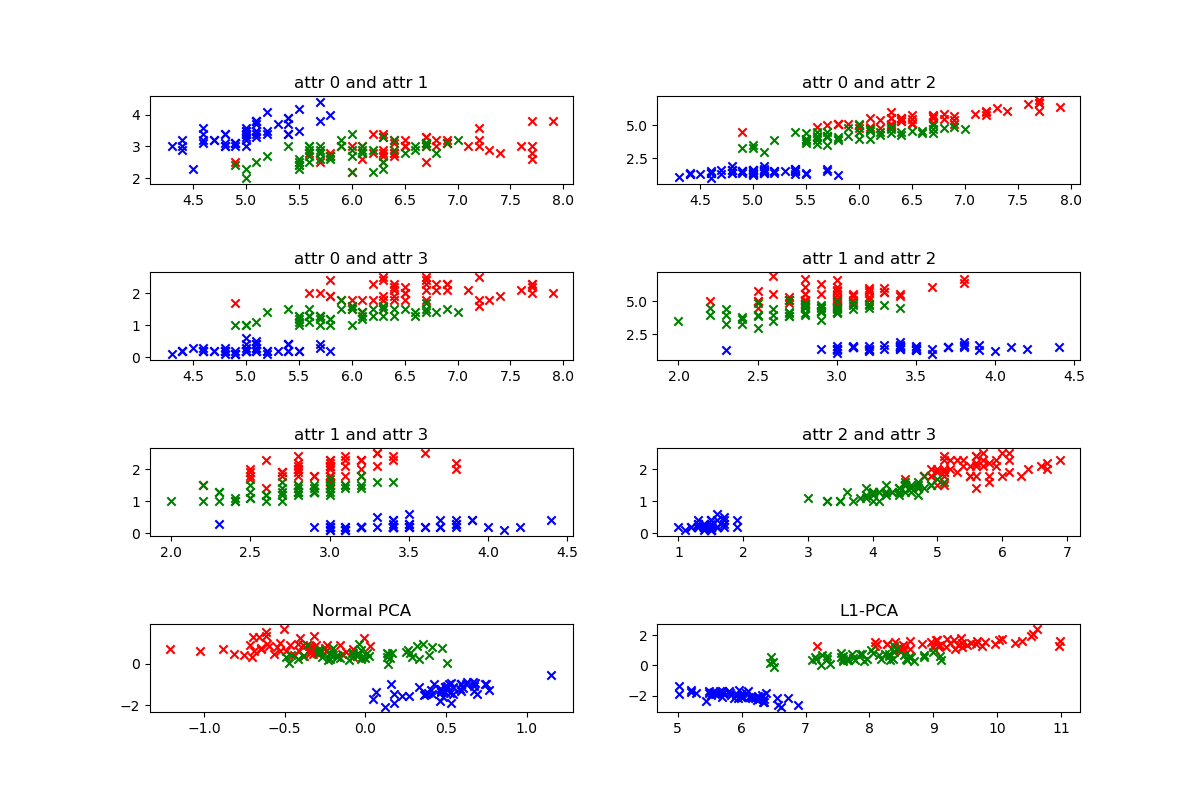
[学习笔记] L1-PCA的更多相关文章
- 机器学习实战(Machine Learning in Action)学习笔记————09.利用PCA简化数据
机器学习实战(Machine Learning in Action)学习笔记————09.利用PCA简化数据 关键字:PCA.主成分分析.降维作者:米仓山下时间:2018-11-15机器学习实战(Ma ...
- Deep Learning(深度学习)学习笔记整理系列之(五)
Deep Learning(深度学习)学习笔记整理系列 zouxy09@qq.com http://blog.csdn.net/zouxy09 作者:Zouxy version 1.0 2013-04 ...
- Deep Learning(深度学习)学习笔记整理系列之(四)
Deep Learning(深度学习)学习笔记整理系列 zouxy09@qq.com http://blog.csdn.net/zouxy09 作者:Zouxy version 1.0 2013-04 ...
- Deep Learning深入研究整理学习笔记五
Deep Learning(深度学习)学习笔记整理系列 zouxy09@qq.com http://blog.csdn.net/zouxy09 作者:Zouxy version 1.0 2013-04 ...
- 概率图模型学习笔记:HMM、MEMM、CRF
作者:Scofield链接:https://www.zhihu.com/question/35866596/answer/236886066来源:知乎著作权归作者所有.商业转载请联系作者获得授权,非商 ...
- tensorflow学习笔记——使用TensorFlow操作MNIST数据(2)
tensorflow学习笔记——使用TensorFlow操作MNIST数据(1) 一:神经网络知识点整理 1.1,多层:使用多层权重,例如多层全连接方式 以下定义了三个隐藏层的全连接方式的神经网络样例 ...
- tensorflow学习笔记——自编码器及多层感知器
1,自编码器简介 传统机器学习任务很大程度上依赖于好的特征工程,比如对数值型,日期时间型,种类型等特征的提取.特征工程往往是非常耗时耗力的,在图像,语音和视频中提取到有效的特征就更难了,工程师必须在这 ...
- Oracle学习笔记三 SQL命令
SQL简介 SQL 支持下列类别的命令: 1.数据定义语言(DDL) 2.数据操纵语言(DML) 3.事务控制语言(TCL) 4.数据控制语言(DCL)
- Java学习笔记(04)
Java学习笔记(04) 如有不对或不足的地方,请给出建议,谢谢! 一.对象 面向对象的核心:找合适的对象做合适的事情 面向对象的编程思想:尽可能的用计算机语言来描述现实生活中的事物 面向对象:侧重于 ...
- Linux 学习笔记
Linux学习笔记 请切换web视图查看,表格比较大,方法:视图>>web板式视图 博客园不能粘贴图片吗 http://wenku.baidu.com/view/bda1c3067fd53 ...
随机推荐
- (๑•̀ㅂ•́)و✧QQ用户信息管理系统
这是第二篇文章,就直接切主题 这次剖析的也是自己的作业之一:QQ信息管理系统 一:(此处省略了建Proarams类,其实目的只是想强调把连接语句单独放一个类里更容易调用,命名规范如图) 二:(导入SQ ...
- Python之if-else语句
if--else语句if username == 'admin' and password == '123456': print('身份验证成功!') else: print('身份验证失败!')if ...
- 【死磕 Java 集合】— ConcurrentSkipListMap源码分析
转自:http://cmsblogs.com/?p=4773 [隐藏目录] 前情提要 简介 存储结构 源码分析 主要内部类 构造方法 添加元素 添加元素举例 删除元素 删除元素举例 查找元素 查找元素 ...
- MySQL 数据类型简介 创建数据表及其字段约束
数据类型介绍 MySQL 数据类型分类 整型 浮点型 字符类型(char与varchar) 日期类型 枚举与集合 具体数据类型见这篇博客 MySQL表操作中的约束 primary key 主键约束 非 ...
- 1.Lucene简介
1.Lucene简介 Lucene是一个基于Java的全文信息检索工具包,它不是一个完整的搜索应用程序,而是为你的应用程序提供索引和搜索功能 Lucene是开源项目,它是可扩展,高性能的库用于索引和搜 ...
- 解决canvas图片getImageData,toDataURL跨域问题
图片服务器需要配置Access-Control-Allow-Origin 当需要需要对canvas图片进行getImageData()或toDataURL()操作的时候,跨域问题就出来了.图片服务器需 ...
- 从零开始实现一个简易的Java MVC框架(三)--实现IOC
Spring中的IOC IoC全称是Inversion of Control,就是控制反转,他其实不是spring独有的特性或者说也不是java的特性,他是一种设计思想.而DI(Dependency ...
- vue 中echart折线自适应
前端时间做一个vue的项目,echart是按需引入的如下: // 引入 ECharts 主模块 import echarts from 'echarts/lib/echarts' // 引入折线图 i ...
- 1024·程序员节来啦!MyEclipse致敬改变世界的程序猿
1024·程序员狂欢季 MyEclipse/CodeMix — Java开发利器!现金红包免费领! 快拆开看你的最大优惠券是多少,幸运奖红包翻倍! (活动期间在线下单的客户才可享受此优惠,过期恢复 ...
- Vue-指令补充、过滤器、计数器属性、监听属性
vue实例成员: el | template |data | methods watch 监听事件| computed 计数属性使用 | filters过滤器 | props 父传子 componen ...
