git合并分支与解决冲突
前提:
当前开发的分支为feature/20161129_317606_algoplatform_1,由于feature/20161130_322574_tmstools_1分支有新内容,所以准备将feature/20161130_322574_tmstools_1分支合并到feature/20161129_317606_algoplatform_1分支上
步骤:
1、当前在feature/20161129_317606_algoplatform_1分支,fetch准备合并的分支feature/20161130_322574_tmstools_1

2、fetch好了以后,查看本地都有哪些分支,主要是确认要合并的两个分支是否都在本地

3、使用git merge合并分支,如果有冲突会提示

4、查看状态,可以看出更加清楚的看出哪些文件因为冲突没有被合并,然后去解决冲突
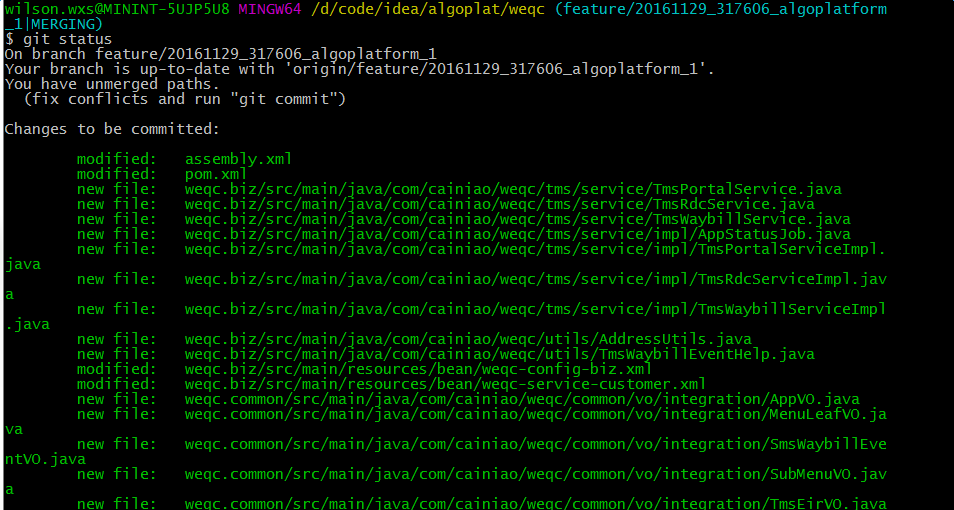

5、解决好冲突后,提交文件,将文件push到远程feature/20161129_317606_algoplatform_1的分支上去
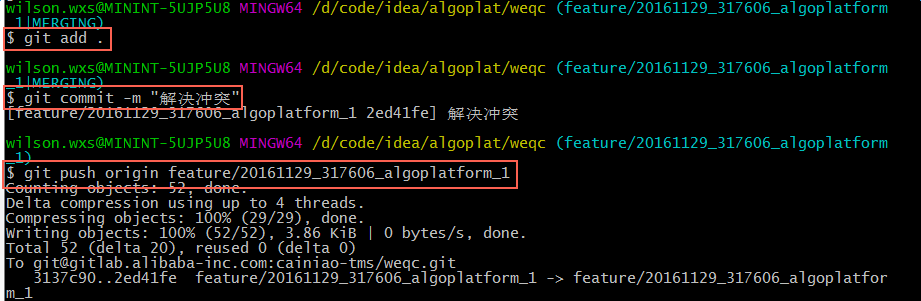
6、查看状态,本地都已更新,合并成功!

git合并分支与解决冲突的更多相关文章
- Git合并分支出现的冲突解决
人生不如意之事十有八九,合并分支往往也不是一帆风顺的. 我们准备新的分支newbranch. LV@LV-PC MINGW32 /c/gitskill (master)$ git checkout - ...
- GIT 分支管理:创建与合并分支、解决合并冲突
分支就是科幻电影里面的平行宇宙,当你正在电脑前努力学习Git的时候,另一个你正在另一个平行宇宙里努力学习SVN. 如果两个平行宇宙互不干扰,那对现在的你也没啥影响.不过,在某个时间点,两个平行宇宙合并 ...
- Git 解决合并分支时的冲突
参考链接:https://www.liaoxuefeng.com/wiki/896043488029600/900004111093344 创建分支时,新分支的文件内容建立在原分支的基础上,我们称这时 ...
- git 合并分支到master
git 合并分支到master 假如我们现在在dev分支上,刚开发完项目,执行了下列命令 git add .git commit -m ‘dev'git push -u origin dev 然后 ...
- 用git合并分支时,如何保持某些文件不被合并
用git合并分支时,如何保持某些文件不被合并_fkaking的专栏-CSDN博客_git 合并分支 https://blog.csdn.net/fkaking/article/details/4495 ...
- eclipse git如何切换分支,拉取代码,合并代码,解决冲突等
(如果想看eclipse拉取git项目,移步到我上一篇文章)以下步骤是eclipse运用git的切换分支,拉取合并代码的基本操作: 1.切换远程分支:鼠标右键项目--team--switch to - ...
- Git合并分支或者冲突
假设冲突文件是 test/TestCase.php 下面分5种情况讨论. 1.本地不变. 然后远程别人有更新. git pull 这种最简单,没有冲突,本地工作区直接更新 2.我本 ...
- Git 分支管理 解决冲突
人生不如意之事十之八九,合并分支往往也不是一帆风顺的. 准备新的feature1分支,继续我们的新分支开发: $ git checkout -b feature1 -- 在feature1分支上修改r ...
- Git合并分支命令:git merge --ff
今天研究了一下git merge命令常用参数,并分别用简单的例子实验了一下,整理如下: 输入git merge -h可以查看相关参数: --ff 快速合并,这个是默认的参数.如果合并过程出现冲突,G ...
随机推荐
- UML_visio安装及使用
安装:百度云安装visio 64bit 类图在visio当中 用例图 来自为知笔记(Wiz)
- LeetCode:前K个高频单词【692】
LeetCode:前K个高频单词[692] 题目描述 给一非空的单词列表,返回前 k 个出现次数最多的单词. 返回的答案应该按单词出现频率由高到低排序.如果不同的单词有相同出现频率,按字母顺序排序. ...
- 14链表中倒数第k个结点
题目描述 输入一个链表,输出该链表中倒数第k个结点. 思路: 快慢指针 快指针 先走k 步, 然后快慢指针一起走 当快指针走到null 时, 慢指针就是所求的倒数第k个节点 tips: 判断k是否 ...
- nodejs多核处理
前言大家都知道nodejs是一个单进程单线程的服务器引擎,不管有多么的强大硬件,只能利用到单个CPU进行计算.所以,有人开发了第三方的cluster,让node可以利用多核CPU实现并行. 随着nod ...
- mfc学习---文档视图架构
MFC的AppWizard可以生成三种类型的应用程序:基于对话框的应用.单文档应用(SDI)和多文档应用(MDI). 一般情况下,采用文档/视结构的应用程序至少应由以下对象组成: 1. ...
- 理解音视频 PTS 和 DTS
视频 视频的播放过程可以简单理解为一帧一帧的画面按照时间顺序呈现出来的过程,就像在一个本子的每一页画上画,然后快速翻动的感觉. 但是在实际应用中,并不是每一帧都是完整的画面,因为如果每一帧画面都是完整 ...
- CSS3小图标菜单导航
在线演示 本地下载
- Vmware ESXi 6.0 多Vlan部署,vSphere Client管理方法
背景: 公司IT部门新购了两台服务器与一台存储,打算做虚拟化,并将存储分成两个部分,分别配给那两台服务器.在宿主机上要安装的虚拟机属于不同的网段,这就涉及了多VLAN,当然这并不是多么高深的技术,属于 ...
- openstack认证实践
环境: 客户端:负责发送请求, 服务器:负责接受请求: 认证服务器keystone:负责认证 具体认证步骤: 1.客户端首先进行签名计算,将得到的签名字符串作为authorization发给keyst ...
- LeetCode——Hamming Distance
LeetCode--Hamming Distance Question The Hamming distance between two integers is the number of posit ...
