从Softmax回归到Logistic回归

　　Softmax回归是Logistic回归在多分类问题上的推广，是有监督的。

　　回归的假设函数（hypothesis function）为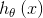，我们将训练模型参数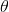，使其能够最小化代价函数：

　　　　　　　　

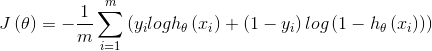
在Softmax回归中，我们解决的是多分类问题，类标y可以取k个不同的值。对于给定的测试输入x，我们想用假设函数针对每一个类别j估算出概率值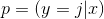。也就是说，我们想估计x的每一种分类结果的概率。因此，我们的假设函数将要输出一个k维的向量（向量元素的和为1）来表示这k个估计的概率值。具体地说，我们的假设函数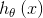形式如下：

　　　　　　　　

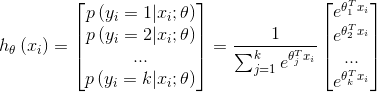
其中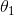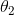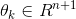，，···，是模型参数。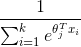这一项对概率分布进行归一化，使得所有的概率之和为1。

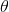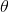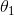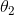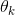　　为了方便起见，我们同样使用符号来表示全部的模型参数。在实现softmax回归时，将用一个的矩阵来表示会很方便，该矩阵是将，，···，按行罗列起来得到的，如下表示：

　　　　　　　　

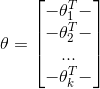
代价函数

　　现在介绍softmax回归算法的代价函数。在下面的公式中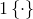，是示性函数，其取值规则为：1{值为真的表达式}=1，1{值为假的表达式}=0。代价函数为：

　　　　　　　　

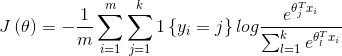
上述公式是logistic回归代价函数的推广。可以看到，softmax代价函数与logistic代价函数在形式上非常类似，只是在softmax代价函数中对类标记的k个可能值进行了累加。注意在softmax回归中将x分类为类别j的概率为：

　　　　　　　　

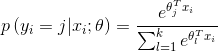
对于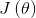的最小化问题，目前还没有闭式解决。因此，我们使用迭代的优化算法（例如梯度下降法，或L-BFGS）。经过求导，我们得到梯度公式如下：

　　　　　　　　

有了上述偏导数公式后，我们就可以将它带入到梯度下降法等算法中，来最小化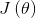。在实现softmax回归算法时，我们通常会使用上述代价函数的一个改进版本。具体来说，就是和权重衰减（weight decay）一起使用。我们接下来介绍使用它的动机和细节。

　　softmax回归有一个不寻常的特点：它有一个“冗余”的参数集。为了便于阐述这一特点，假设我们从参数向量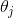中减去了向量，这时，每一个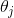都变成了。此时假设函数变成了

　　　　　　　　

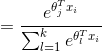
也就是说，从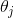中减去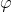完全不影响假设函数的预测结果。这表明前面的softmax回归模型中存在冗余的参数。更正式一点来说，softmax模型被过度参数化了。对于任意一个用于拟合数据的假设函数 ，可以求出多组参数值，这些参数得到的是完全相同的假设函数。

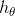　　进一步而言，如果参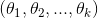数是代价函数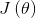的极小值点，那么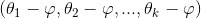同样也是它的极小值点，其中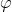可以为任意向量。因此使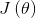最小化的解不是唯一的。（有趣的是，由于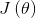仍然是一个凸函数，因此梯度下降时不会遇到局部最优解的问题。但是Hessian矩阵是奇异的/不可逆的，这会导致采用牛顿法优化就遇到数值计算的问题。）

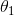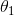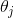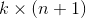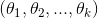　　注意，当时，我们总是可以将替换为（即替换为全零向量），并且这种变换不会影响假设函数。因此我们可以去掉参数向量（或者其他中的任意一个）而不影响假设函数的表达能力。实际上，与其优化全部的个参数（其中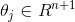），我们可以令，只优化剩余的个参数，这样算法依然能够正常工作。

　　在实际应用中，为了使算法实现更简单清楚，往往保留所有参数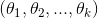，而不任意地将某一参数设置为0。但此时我们需要对代价函数做一个改动：加入权重衰减。权重衰减可以解决softmax回归的参数冗余所带来的数值问题。

权重衰减

　　我们通过添加一个权重衰减项

　　　　　　　　

来修改代价函数，这个衰减项会惩罚过大的参数值，现在我们的代价函数变为：

　　　　　　　　

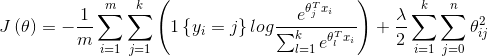
有了这个权重衰减项以后，代价函数就变成了严格的凸函数，这样就可以保证得到唯一的解了。此时的Hessian矩阵变为可逆矩阵，并且因为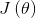是凸函数，梯度下降法和L-BFGS等算法可以保证收敛到全局最优解。

　　通过最小化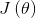，我们就能实现一个可用的softmax回归模型。

Softmax回归和Logistic回归的关系

　　当类别数时，softmax回归退化为logistic回归，这表明softmax回归是logistic回归的一般形式。具体地说，当时，softmax回归的假设函数为

　　　　　　　　

利用softmax回归参数冗余的特点，我们令，并且从两个参数向量都减去向量，得到

　　　　　　　　

　　　　　　　　　　　　

　　　　　　　　　　　　

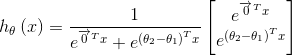
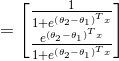
因此，用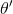来表示，我们会发现softmax回归器预测其中一个类别的概率为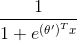，另一个类别的概率为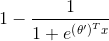，这与logistic回归是一致的。

Softmax回归 vs. k个二元分类器

　　如果你在开发一个音乐分类的应用，需要对k种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 k 个独立的二元分类器呢？

　　这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为5。）

　　如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。

　　现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？

　　在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器 。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。

参考资料

http://ufldl.stanford.edu/wiki/index.php/UFLDL_Tutorial