CSAPC08台湾邀请赛_T1_skyline

题目链接：CSAPC08台湾邀请赛_T1_skyline

题目描述

一座山的山稜线由许多片段的45度斜坡构成，每一个片段不是上坡就是下坡。

/ *

/​ * * /

​/ * /\ //

​/ // /

在我们眼前的所见的任何宽度为n个单位的山稜形状，可以轻松地观察到所有山顶的位置。

请问有多少种山稜线的形状，使得所有山顶的位置由左而右非递减呢？

所有的山稜线都必须完整，也就是说左右两端都必须是高度为0的山脚，而且不能有任何山谷的位置隐没在地平线底下。

输入输出格式

输入格式

输入仅包含一个数字n，n一定会是偶数，因为会有相同片段数量的上坡以及下坡。

输出格式

请输出山顶位置由左而右非递减的山稜线形状总数。

由于答案可能很大，你只要输出以十进位表示时，它的最后9位数即可。

样例

INPUT

6

OUTPUT

4

HINT

佔总分20%的测试数据中 n<=60

佔总分40%的测试数据中 n<=200

佔总分100%的测试数据中 n<=3000

SOLUTION

这题考场上耗了我大半的时间还没搞出来qwq。

首先，根据题意分析，很容易就能看出这是个区间dp。

区间dp怎么传递呢？看到题目要求：求宽度为\(n\)，山顶高度非降的方案和。所以我们可以开一个二维数组\(dp[i][j]\)记录答案：第一维\(i\)用来记录限定条件：“宽度”；第二维\(j\)来记录限定条件：这些山峰的最高高度\(j\)，以便转移。

但是啊，我们的\(dp\)数组只能记录最高高度为\(j\)的情况，那如果我要拓宽宽度的话，肯定是不能再把所有的最高高度的情况又重新枚举累加的，所以考虑用一个前缀和数组\(sum[i][j]\)来记录宽度为\(i\)，最高高度限定为\(j\)（可以小于\(j\)）的所有情况，可以说\(sum\)数组就是把宽度为\(i\)的所有合法情况记录了下来。

接下来就是转移了。

首先我们有两大种情况：

Ⅰ.我们的\(dp[i][j]\)的情况可以直接由\(dp[i-1][j-1]\)的情况得到；

这就相当于可以想象把\(dp[i-1][j-1]\)中包含的山的情况整体往上拱了一层。如下图：

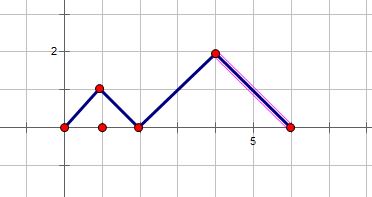
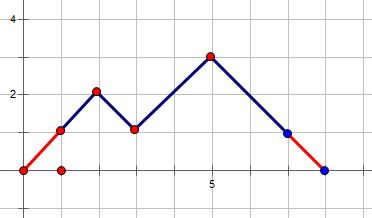
Ⅱ.我们也可以通过在\(sum[i-2][j]\)的基础上加上一座最小的山。如下图：

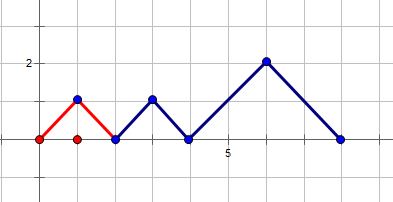
因为\(sum[i-2][j]\)加上一座单位高度的小山已经把类似于最低山的高度大于单位长度的所有情况考虑了进来，而我们的情况Ⅰ就是对应着这种“最低山的高度大于单位长度”的所有情况。

所以任何情况已经可以用以上两种情况相互叠加着表示，可以保证的是这么算目前已经没有遗漏了。

但其实还会存在一个小问题。

在整体宽度为\(i+j\)时，假设我们的右边有一座高度为\(j\)的山峰，那么显然地，这座山峰的宽度为\(2j\)，所以去掉右边的山峰后，我们左边部分的山峰宽度为\(i-j\)，那么我们的\(sum[i-2j][j]\)就可以表示当前说的这种情况的所有方案，此时是合法的。

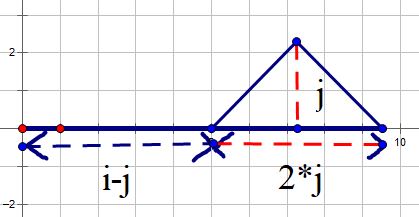
不过我们若将左边部分的宽度减少一个单位匀给右边部分，右边部分一定不能在保持只有一座山峰的情况下保证最高高度为\(j\)，所以不合法。

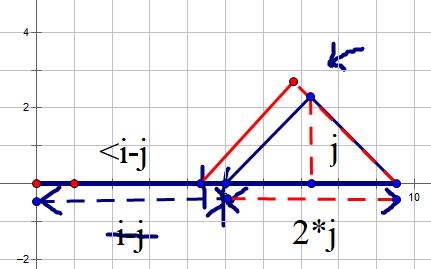
但是可能会有点想不通的是：为什么右边就一定只能有一座山峰呢？

其实，注意一下我们的转移方程，我们的\(sum[i-2][j]\)是通过和一个单位高度的山峰组合在一起作为答案加进我们的\(dp\)数组里去的，然后当我们的单位高度小山峰被垫高到了高度\(j\)时，与它同组搭配的\(sum\)数组的组合情况就必须考虑一下其合法性了，因为这种非法组合也本来就不能算在答案里。于是考虑删除。

代码就在下面，这篇题解其实更多就是对下面的代码的解释因为这个标程一点注释都没有啊。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
using namespace std;
const int N=3010;
const int P=1000000000;
int n,dp[N][N],sum[N][N];
int main(){
	int i,j;
	memset(dp,0,sizeof(dp));memset(sum,0,sizeof(sum));
	dp[1][1]=1;sum[1][1]=1;
	for (i=2;i<=3000;++i){
		for (j=1;j<i;++j){
			if ((i+j)%2==0){
				dp[i][j]=(dp[i-1][j-1]+sum[i-2][j])%P;
				if (i-j-j>0) {dp[i][j]=(dp[i][j]-sum[i-j-j-1][j]+P)%P;}
			}
			sum[i][j]=(sum[i-1][j]+dp[i][j])%P;
		}
		dp[i][i]=1;sum[i][i]=1;
	}
	while (scanf("%d",&n)!=EOF){
		int ans=0;
		for (i=1;i<=n/2;++i) {ans=(ans+dp[n-i][i])%P;}
		printf("%d\n",ans);
	}
	return 0;
}