PAT Advanced 1003 Emergency (25) [Dijkstra算法]

题目

As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.

Input Specification

Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (<=500) – the number of cities (and the cities are numbered from 0 to N-1), M – the number of roads, C1 and C2 – the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1, c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.

Output Specification

For each test case, print in one line two numbers: the number of diferent shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.

Sample Input

5 6 0 2

1 2 1 5 3

0 1 1

0 2 2

0 3 1

1 2 1

2 4 1

3 4 1

Sample Output

2 4

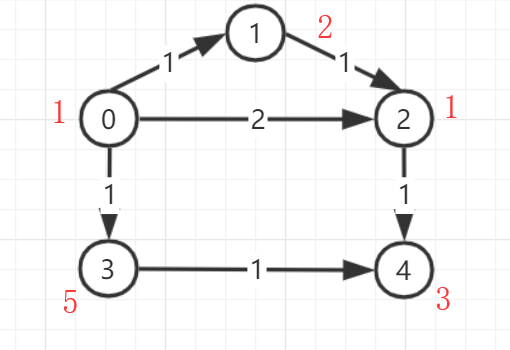
题意

国家紧急救援组织的小组分布在全国各个城市，地图标出了每个城市的救援小组数目和城市间的公路（稀疏城市），若出现紧急情况，需要从当前城市出发走最短路径（标准：耗时最短）到达需要救援的城市，同时，要求路上能尽量找到更多帮手协助救援

输入：顶点和边，领导组所在城市，各个城市急救小组的数目

输出：最短路径数目和能找到最多救援小组助手的数目

题目分析

已知网图点权-城市急救小组数目，边权-城市间路程耗时，求最短路径，要求该最短路径点权和最大

输入：顶点，点权，边，边权

输出：最短路径数目 所有最短路径中最大点权和

解题思路

1. 存储图

存储边和边权

1.1 邻接表（题目已知稀疏图，用邻接表比较合适）

1.2 邻接矩阵

存储点权

整型数组

2. 求最短路径

• Dijkstra算法求最短路径，每次收集一个顶点到最短路径中时，若使得起点到其他顶点的最短路径更短，则更新dist[i]，若等于dist[i]，需比较其点权和，若点权和更大则更新dist[i]；

注：本题不需要记录路径，int path[n]可以省略

Code

Code 01（邻接表）

#include <iostream>
#include <vector>
using namespace std;
const int maxn=510;
const int INF=9999999;
int n,c1,c2,vw[maxn]; //g边；vw点权
int dist[maxn],col[maxn];// col已经找到最小路径的顶点收集到col中
int w[maxn],num[maxn];
struct node{
	int v;
	int w;
};
vector<node> gw[maxn]; //gw边权；
/* dijkstra算法 求最短路径 */
int dmin() {
	int min=INF,mini=0;
	for(int i=0; i<n; i++) {
		if(col[i]==1)continue; // 跳过被收集的点
		if(min>dist[i]) {
			min=dist[i]; //没有被收集的顶点中的最小者
			mini=i;
		}
	}
	return mini;
}
void dijkstra(int c) {
	fill(dist,dist+n,INF);
	dist[c]=0;
	num[c]=1; //起点c1到其直连的顶点，都只有一条最短路径
	w[c]=vw[c]; //起点c1的点权
	for(int i=0; i<n; i++) {
		int min=dmin(); //当前dist中最小值对应的顶点
		if(min==c2) break; //已找到目标顶点
		col[min]=1;
		for(int j=0; j<gw[min].size(); j++) {
			node e = gw[min][j];
			if(col[e.v]==1)continue; //跳过 已被收集的顶点
			if(dist[min]+e.w<dist[e.v]) {
				dist[e.v]=dist[min]+e.w; //更新dist
				w[e.v]=w[min]+vw[e.v]; // 更新c1到j的最短所有路径中的最大权重和
				num[e.v]=num[min]; // 更新c1到j的最短路径数
			} else if(dist[min]+e.w==dist[e.v]) {
				if(w[min]+vw[e.v]>w[e.v])
					w[e.v]=w[min]+vw[e.v];
				num[e.v]+=num[min];
			}
		}
	}
}
int main(int argc,char * argv[]) {
	int m,a,b,r;
	scanf("%d %d %d %d",&n,&m,&c1,&c2);
	for(int i=0; i<n; i++)
		scanf("%d",&vw[i]); //点权
	for(int i=0; i<m; i++) {
		scanf("%d %d %d",&a,&b,&r);
		gw[a].push_back({b,r});
		gw[b].push_back({a,r});
	}
	dijkstra(c1);
	printf("%d %d",num[c2],w[c2]);
	return 0;
}

Code 02

#include <iostream>
using namespace std;
const int maxn=510;
const int INF=9999999;
int n,c1,c2,gw[maxn][maxn],vw[maxn]; //g边；gw边权；vw点权
int dist[maxn],col[maxn];// col已经找到最小路径的顶点收集到col中
int w[maxn],num[maxn];
/* dijkstra算法 求最短路径 */
int dmin() {
	int min=INF,mini=0;
	for(int i=0; i<n; i++) {
		if(col[i]==1)continue; // 跳过被收集的点
		if(min>dist[i]) {
			min=dist[i]; //没有被收集的顶点中的最小者
			mini=i;
		}
	}
	return mini;
}
void dijkstra(int c) {
	fill(dist,dist+n,INF);
	dist[c]=0;
	num[c]=1; //起点c1到其直连的顶点，都只有一条最短路径
	w[c]=vw[c]; //起点c1的点权
	for(int i=0; i<n; i++) {
		int min=dmin(); //当前dist中最小值对应的顶点
		if(min==c2) break; //已找到目标顶点
		col[min]=1;
		for(int j=0; j<n; j++) {
			if(gw[min][j]==0||col[j]==1)continue; //跳过 已被收集的顶点
			if(dist[min]+gw[min][j]<dist[j]) {
				dist[j]=dist[min]+gw[min][j]; //更新dist
				w[j]=w[min]+vw[j]; // 更新c1到j的最短所有路径中的最大权重和
				num[j]=num[min]; // 更新c1到j的最短路径数
			} else if(dist[min]+gw[min][j]==dist[j]) {
				if(w[min]+vw[j]>w[j])
					w[j]=w[min]+vw[j];
				num[j]+=num[min];
			}
		}
	}
}
int main(int argc,char * argv[]) {
	int m,a,b,r;
	scanf("%d %d %d %d",&n,&m,&c1,&c2);
	for(int i=0; i<n; i++)
		scanf("%d",&vw[i]); //点权
	for(int i=0; i<m; i++) {
		scanf("%d %d %d",&a,&b,&r);
		gw[a][b]=gw[b][a]=r; //边权
	}
	dijkstra(c1);
	printf("%d %d",num[c2],w[c2]);
	return 0;
}