Java实现DFS深度优先查找

1 问题描述

深度优先查找（depth-first search，DFS）可以从任意顶点开始访问图的顶点，然后把该顶点标记为已访问。在每次迭代的时候，该算法紧接着处理与当前顶点邻接的未访问顶点。这个过程一直持续，直到遇到一个终点——该顶点的所有邻接顶点都已被访问过。在该终点上，该算法沿着来路后退一条边，并试着继续从那里访问未访问的顶点。再后退到起始顶点上，并且起始顶点也是一个终点时，该算法最终停了下来。这样，起始顶点所在的连通分量的所有顶点都被访问过了。如果，未访问过的顶点仍然存在，该算法必须从其中任一点开始，重复上述过程。

总之，记住一句话，深度优先查找就是先尽可能达到当前遍历路径能够达到最长的路径，一旦达到该路径终点，再回溯，从原来已遍历过顶点（PS：该顶点包含多个分支路径）处开始新的分支路径遍历。

2 解决方案

2.1 蛮力法

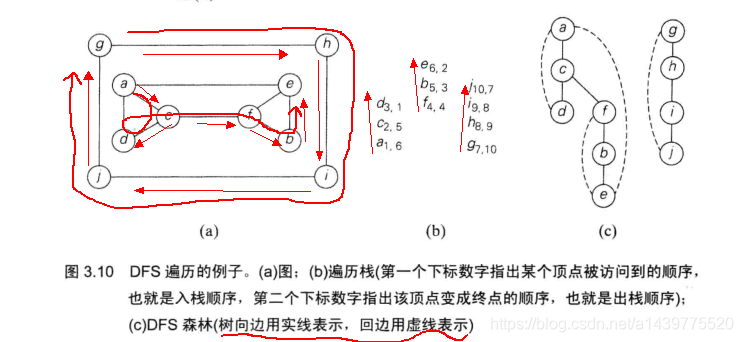
此处借用算法设计与分析基础（第三版）上一段概念介绍，及说明图形介绍其具体遍历过程，下面的具体代码使用数据就是下图中相关数据。

package com.liuzhen.chapterThree;

public class DepthFirstSearch {
    public int count = 0;    //用于计算遍历总次数
     /*
      * adjMatrix是待遍历图的邻接矩阵
      * value是待遍历图顶点用于是否被遍历的判断依据，0代表未遍历，非0代表已被遍历
      * result用于存放深度优先遍历的顶点顺序
      */
    public void dfs(int[][] adjMatrix,int[] value,char[] result){
        for(int i = 0;i < value.length;i++){
            if(value[i] == 0){
                char temp = (char) ('a' + i);
                System.out.println();
                System.out.println("深度为："+i+"，当前出发点："+temp);
                result[i] = temp;                //存放当前正在遍历顶点下标字母
                dfsVisit(adjMatrix,value,result,i);
            }
        }
    }
     /*
     * adjMatrix是待遍历图的邻接矩阵
     * value是待遍历图顶点用于是否被遍历的判断依据，0代表未遍历，非0代表已被遍历
     * result用于存放深度优先遍历的顶点顺序
     * number是当前正在遍历的顶点在邻接矩阵中的数组下标编号
     */
    public void dfsVisit(int[][] adjMatrix,int[] value,char[] result,int number){
        value[number] = ++count;               //把++count赋值给当前正在遍历顶点判断值数组元素，变为非0，代表已被遍历
        System.out.print("当前已行走顶点value["+number+"] = "+value[number]+"  ");
        for(int i = 0;i < value.length;i++){
            if(adjMatrix[number][i] == 1 && value[i] == 0){          //当当前顶点的相邻有相邻顶点可行走且其为被遍历
                char temp = (char) ('a' + i);
                result[count] = temp;        //存放即将行走的顶点下标字母
                System.out.println(" 当前i值："+i+" 到达"+temp+"地");
                dfsVisit(adjMatrix,value,result,i);   //执行递归，行走第i个顶点
            }
        }
    }

    public static void main(String[] args){
        int[] value = new int[10];              //初始化后，各元素均为0
        char[] result = new char[10];
        int[][] adjMatrix = {{0,0,1,1,1,0,0,0,0,0},
                {0,0,0,0,1,1,0,0,0,0},
                {1,0,0,1,0,1,0,0,0,0},
                {1,0,1,0,0,0,0,0,0,0},
                {1,1,0,0,0,1,0,0,0,0},
                {0,1,1,0,1,0,0,0,0,0},
                {0,0,0,0,0,0,0,1,0,1},
                {0,0,0,0,0,0,1,0,1,0},
                {0,0,0,0,0,0,0,1,0,1},
                {0,0,0,0,0,0,1,0,1,0}};
        DepthFirstSearch test = new DepthFirstSearch();
        test.dfs(adjMatrix,value,result);
        System.out.println();
        System.out.println("判断节点是否被遍历结果（0代表未遍历，非0代表已被遍历）：");
        for(int i = 0;i < value.length;i++)
            System.out.print("  "+value[i]);
        System.out.println();
        System.out.println("深度优先查找遍历顺序如下：");
        for(int i = 0;i < result.length;i++)
            System.out.print("  "+result[i]);
    }
}

运行结果：

深度为：0，当前出发点：a
当前已行走顶点value[0] = 1   当前i值：2 到达c地
当前已行走顶点value[2] = 2   当前i值：3 到达d地
当前已行走顶点value[3] = 3   当前i值：5 到达f地
当前已行走顶点value[5] = 4   当前i值：1 到达b地
当前已行走顶点value[1] = 5   当前i值：4 到达e地
当前已行走顶点value[4] = 6
深度为：6，当前出发点：g
当前已行走顶点value[6] = 7   当前i值：7 到达h地
当前已行走顶点value[7] = 8   当前i值：8 到达i地
当前已行走顶点value[8] = 9   当前i值：9 到达j地
当前已行走顶点value[9] = 10
判断节点是否被遍历结果（0代表未遍历，非0代表已被遍历）：
 5  2  3  6  4  7  8  9  10
深度优先查找遍历顺序如下：
  a  c  d  f  b  e  g  h  i  j