分布式事务解决方案Seata

Seata全称是Simple Extensible Autonomous Transaction Architecture，是由阿里巴巴开源的具有高性能和易用性的分布式事务解决方案。

微服务中的分布式事务问题

我们的电商系统使用的是微服务架构，由仓库、订单、用户三个微服务组成，三个微服务分别有着自己的本地数据源。开始事务后，每个服务本身能保证数据一致性，但是服务之间将无法保证数据一致性。这也许是很多企业遇到的问题，而Seata就是解决此类问题的。

Seata组织结构

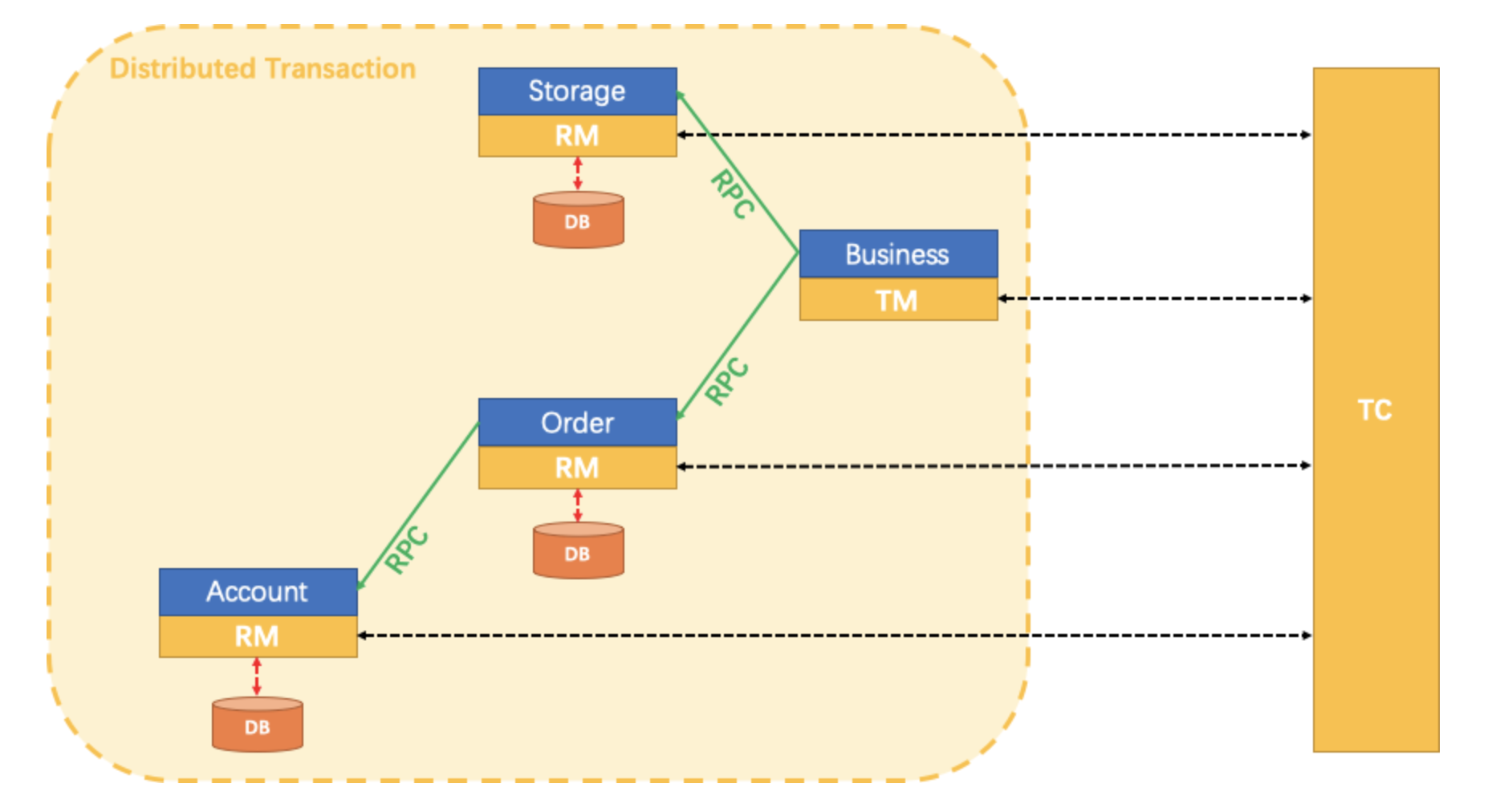
• 事务协调器（TC）：维护全局和分支事务的状态，驱动全局提交或回滚。

• 事务管理器（TM）：定义全局事务的范围：开始全局事务、提交或回滚全局事务。

• 资源管理器（RM）：管理分支事务处理的资源，与TC交谈以注册分支事务和报告分支事务的状态，并驱动分支事务提交或回滚。

Seata管理的分布式事务的典型生命周期

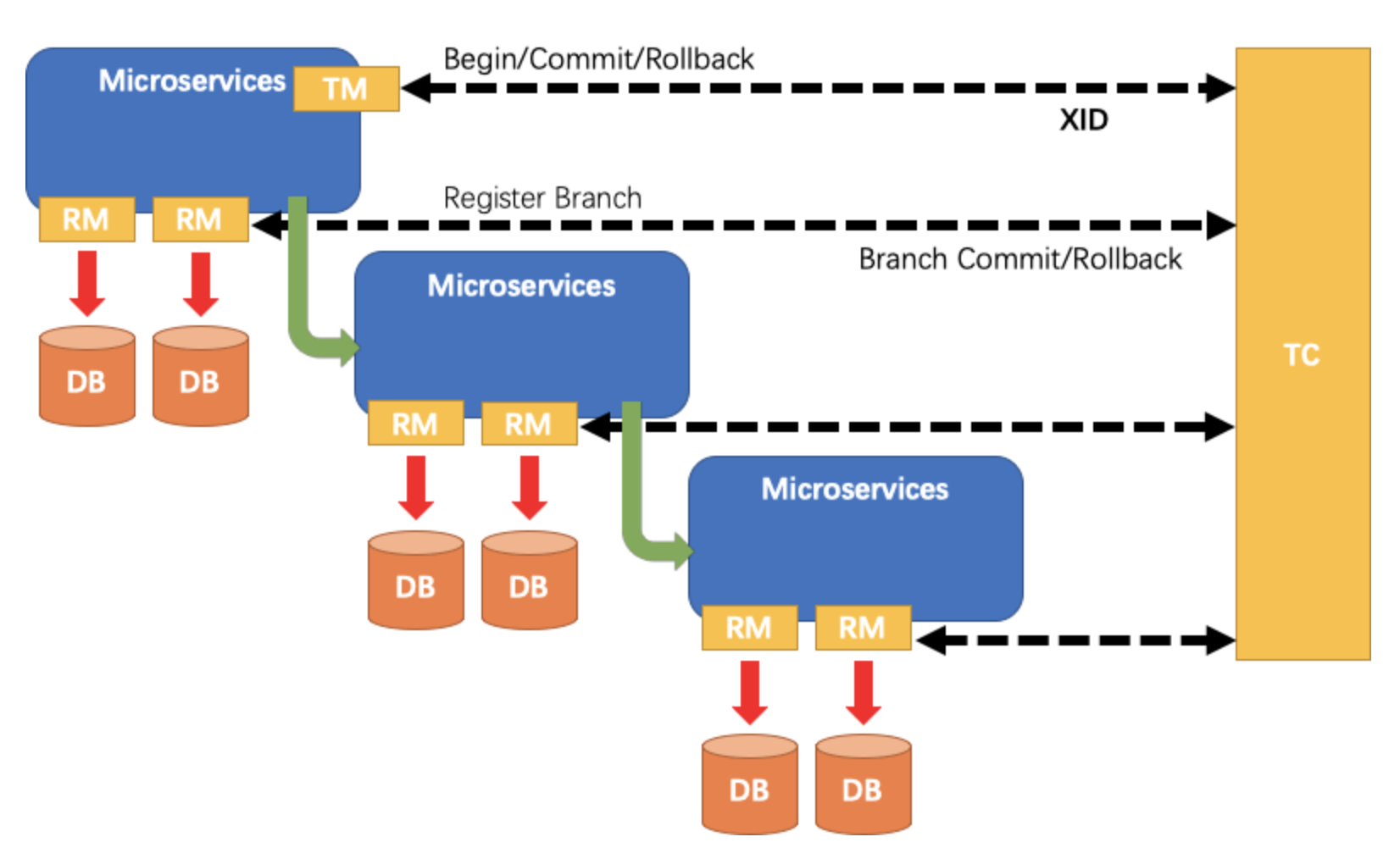
• TM要求TC开始新的全局事务。TC生成代表全局事务的XID。

• XID通过微服务的调用链传播。

• RM将本地事务注册为XID到TC的相应全局事务的分支。

• TM请求TC提交或回滚XID的相应全局事务。

• TC驱动XID对应全局事务下的所有分支事务，完成分支提交或回滚。