[LeetCode] 223.矩形面积

题目链接： https://leetcode-cn.com/problems/rectangle-area

难度：中等

通过率：41.3%

题目描述:

在 二维 平面上计算出两个 由直线构成的 矩形重叠后形成的总面积。

每个矩形由其左下顶点和右上顶点坐标表示，如图所示。

示例:

输入: -3, 0, 3, 4, 0, -1, 9, 2
输出: 45

说明: 假设矩形面积不会超出 **int **的范围。

思路:

这道题，把问题考虑清楚就不难了！

首先，我们调整两个矩形，让第一个矩形是靠最左边的；

其次，先考虑没有重叠的情况，有三种情况，如图所示：

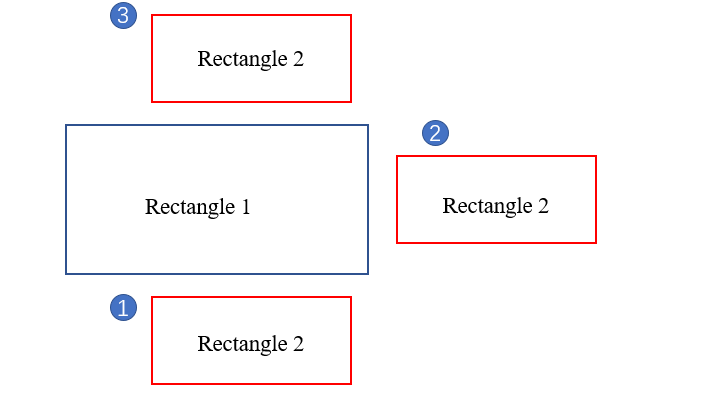
1. rectangle1的下边都大于（等于）rectangle2的上边，即 B >= H
2. rectangle1的右边都小于（等于）rectangle2的左边，即 C >= E
3. rectangle1的上边都小于（等于）rectangle2的下边，即 B >= H

最后， 要考虑重叠的情况，这种其实很好考虑，因为一定有重叠，所以可以找到上下左右边界

上边界，取两个矩形的上边界的最小值

下边界，取两个矩形的下边界的最大值

左边界，取两个矩形的左边界的最大值

右边界，取两个矩形的右边界的最小值

得到重叠面积，只需要两个矩形相加减去重叠面积即可！

---

有疑惑的地方，要留言哦~

代码:

class Solution:
    def computeArea(self, A: int, B: int, C: int, D: int, E: int, F: int, G: int, H: int) -> int:
        # 调整两个矩形位置, 让第一个矩形靠最左边
        if A > E:
            return self.computeArea(E, F, G, H, A, B, C, D)
        # 没有重叠的情况
        if B >= H or D <= F or C <= E:
            return abs(A - C) * abs(B - D) + abs(E - G) * abs(F - H)
        # 重叠情况
        # xia
        down = max(A, E)
        # shang
        up = min(C, G)
        # zuo
        left = max(B, F)
        # you
        right = min(D, H)
        return abs(A - C) * abs(B - D) + abs(E - G) * abs(F - H) - abs(up - down) * abs(left - right)