华为交换机SOCK CPU占用率高处理方法
问题截图:
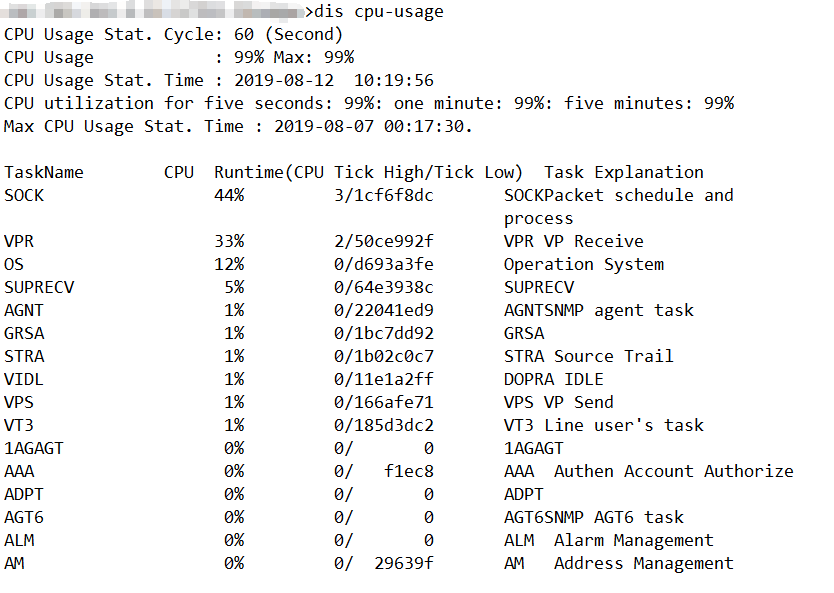
解决方法:
cpu-defend policy cpu
auto-defend enable
auto-defend attack-packet sample 5
auto-defend alarm enable
auto-defend action deny
华为交换机SOCK CPU占用率高处理方法的更多相关文章
- Linux下java进程CPU占用率高分析方法
Linux下java进程CPU占用率高分析方法 在工作当中,肯定会遇到由代码所导致的高CPU耗用以及内存溢出的情况.这种情况发生时,我们怎么去找出原因并解决. 一般解决方法是通过top命令找出消耗资源 ...
- (转)Linux下java进程CPU占用率高-分析方法
Linux下java进程CPU占用率高-分析方法 原文:http://itindex.net/detail/47420-linux-java-%E8%BF%9B%E7%A8%8B?utm_source ...
- Linux下java进程CPU占用率高分析方法(一)
Linux下java进程CPU占用率高分析方法 在工作当中,肯定会遇到由代码所导致的高CPU耗用以及内存溢出的情况.这种情况发生时,我们怎么去找出原因并解决. 一般解决方法是通过top命令找出消耗资源 ...
- CPU占用率高分析方法步骤[转载]
由于涉及到私有代码,所有图片都隐去 1.执行TOP命令,确认CPU占用较高的进程PID 根据top命令,发现PID为8691的Java进程占用CPU高达3858%,出现故障 2.确认该进程中CPU占用 ...
- Linux下java进程CPU占用率高-分析方法
今天登陆同事的一台gateway 开始以为hive环境登陆不了了,仔细一看看了下是因为机器很卡,我每次等几秒没登陆就ctrl+c了,看了下是有个java进程cpu:340.4% mem:14.6% ...
- Linux下CPU占用率高分析方法
一般解决方法是通过top命令找出消耗资源高的线程id,利用strace命令查看该线程所有系统调用1. 通过top命令找到可疑进程PID top - 09:37:18 up 70 days, 16:29 ...
- Linux下java进程CPU占用率高分析方法(二)
1. 通过 top 命令查看当前系统CPU使用情况,定位CPU使用率超过100%的进程ID:2. 通过 ps aux | grep PID 命令进一步确定具体的线程信息:3. 通过 ps -mp pi ...
- Linux下分析某个进程CPU占用率高的原因
Linux下分析某个进程CPU占用率高的原因 通过top命令找出消耗资源高的线程id,利用strace命令查看该线程所有系统调用 1.top 查到占用cpu高的进程pid 2.查看该pid的线程 ...
- Java CPU占用率高分析
首先,通过top命令找出CPU占用率高的进程: 然后,通过ps -o THREAD,tid,time -mp 2066命令找出执行时间最长的线程的TID 将有问题的TID转为16进制格式: print ...
随机推荐
- 什么是UAT
基本概念 UAT,英文User Acceptance Test的简写,也就是用户验收测试,或用户可接受测试,系统开发生命周期方法论的一个阶段,这时相关的用户或独立测试人员根据测试计划和结果对系统进行测 ...
- JavaSE---泛型系统学习
1.概述 1.1.泛型: 允许在 定义 类.接口.方法时 使用 类型形参,这个类型形参 将在声明变量.创建对象.调用方法时 动态地指定: 1.2.jdk5后,引入了 参数化类型(允许程 ...
- [POI2017] Flappy Bird
问题描述 <飞扬的小鸟>是一款风靡的小游戏.在游戏中,小鸟一开始位于(0,0)处,它的目标是飞到横坐标为X的某个位置上.每一秒,你可以选择点击屏幕,那么小鸟会从(x,y)飞到(x+1,y+ ...
- 【leetcode】1169. Invalid Transactions
题目如下: A transaction is possibly invalid if: the amount exceeds $1000, or; if it occurs within (and i ...
- 前端面试题常考&必考之--清除浮动的方法
浮动 问题:子元素设置了float后,脱离父元素,导致父元素无法撑开?(也就是子元素的高度没有过渡到父元素) 例子: 检查元素的效果: (三种)常用的解决办法: 1>额外标签法,添加一个空的di ...
- CSS3实现三角形和对话框
这是最终实现的效果,类似于微信对话框的样式. 分析一下这个对话框的结构,由一个小三角形和一个长方形构成.长方形很容易就可以实现,重点是如何用CSS3做出一个小三角形. 一.如何生成一个三角形 总结: ...
- 整合spring cloud云架构 - 根据token获取用户信息
根据用户token获取yoghurt信息的流程: /** * 根据token获取用户信息 * @param accessToken * @return * @throws Exception */ @ ...
- mysql SELECT语句 语法
mysql SELECT语句 语法,苏州大理石方箱 作用:用于从表中选取数据.结果被存储在一个结果表中(称为结果集). 语法:SELECT 列名称 FROM 表名称 以及 SELECT * FROM ...
- Bellman-ford算法、SPFA算法求解最短路模板
Bellman-ford 算法适用于含有负权边的最短路求解,复杂度是O( VE ),其原理是依次对每条边进行松弛操作,重复这个操作E-1次后则一定得到最短路,如果还能继续松弛,则有负环.这是因为最长的 ...
- Alexa TOP 100万的域名列表
Alexa是一家专门发布网站世界排名的网站,是亚马逊公司的一家子公司.Alexa每天在网上搜集多达几十亿的网址链接,而且为其中的每一个网站进行了排名. Alexa通过Alexa官网查询好像TOP 50 ...
