【leetcode】1035. Uncrossed Lines

题目如下：

We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw connecting lines: a straight line connecting two numbers A[i] and B[j] such that:

• A[i] == B[j];
• The line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.

Return the maximum number of connecting lines we can draw in this way.

Example 1:

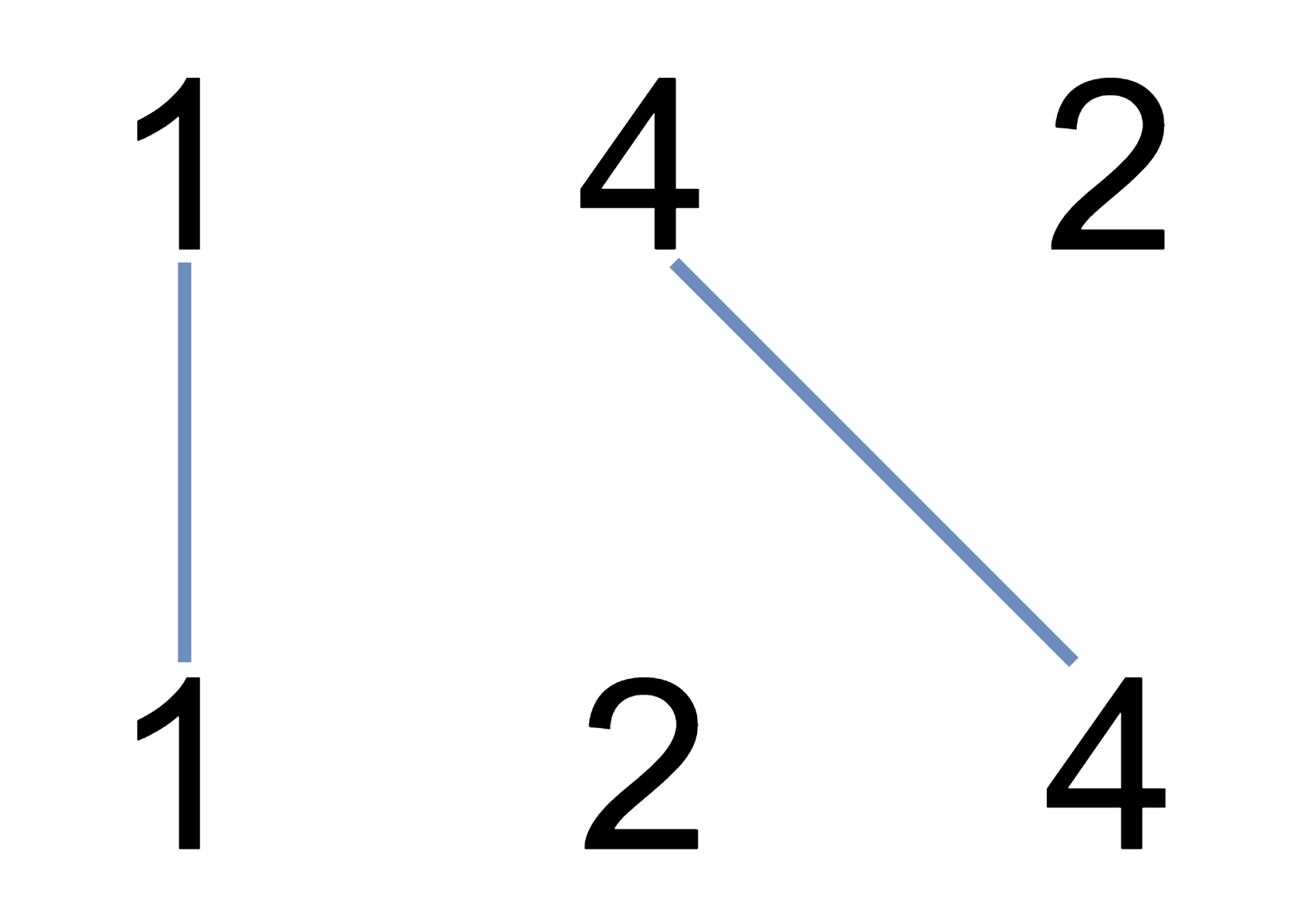
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Example 2:

Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Example 3:

Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

Note:

1. 1 <= A.length <= 500
2. 1 <= B.length <= 500
3. 1 <= A[i], B[i] <= 2000

解题思路：本题可以采用动态规划的方法。记dp[i][j]为A[i]与B[j]连线后可以组成的最多连线的数量，当然这里A[i]与B[j]连线是虚拟的连线，因此存在A[i] != B[j]的情况。首先来看A[i] == B[j]，这说明A[i]与B[i]可以连线，显然有dp[i][j] = dp[i-1][j-1]+1；如果是A[i] != B[j]，那么分为三种情况dp[i][j] = max(dp[i-1][j-1],dp[i][j-1],dp[i-1][j])，这是因为A[i]不与B[j]连线，但是A[i]可能可以与B[j]之前所有点的连线，同理B[j]也是一样的。

代码如下：

class Solution(object):
    def maxUncrossedLines(self, A, B):
        """
        :type A: List[int]
        :type B: List[int]
        :rtype: int
        """
        dp = []
        for i in range(len(A)):
            dp.append([0] * len(B))

        for i in range(len(A)):
            for j in range(len(B)):
                if A[i] == B[j]:
                    dp[i][j] = max(dp[i][j],1)
                    if i - 1 >= 0 and j - 1 >= 0 :
                        dp[i][j] = max(dp[i][j],dp[i-1][j-1]+1)

                else:
                    if i - 1 >= 0 and j - 1 >= 0:
                        dp[i][j] = max(dp[i][j],dp[i-1][j-1])
                    if j - 1 >= 0:
                        dp[i][j] = max(dp[i][j],dp[i][j-1])
                    if i - 1 >= 0:
                        dp[i][j] = max(dp[i][j],dp[i-1][j])
        return dp[-1][-1]