codeforces 979 C. Kuro and Walking Route

C. Kuro and Walking Route

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Kuro is living in a country called Uberland, consisting of $$$n$$$ towns, numbered from $$$1$$$ to $$$n$$$, and $$$n - 1$$$ bidirectional roads connecting these towns. It is possible to reach each town from any other. Each road connects two towns $$$a$$$ and $$$b$$$. Kuro loves walking and he is planning to take a walking marathon, in which he will choose a pair of towns $$$(u, v)$$$ ($$$u \neq v$$$) and walk from $$$u$$$ using the shortest path to $$$v$$$ (note that $$$(u, v)$$$ is considered to be different from $$$(v, u)$$$).

Oddly, there are 2 special towns in Uberland named Flowrisa (denoted with the index $$$x$$$) and Beetopia (denoted with the index $$$y$$$). Flowrisa is a town where there are many strong-scent flowers, and Beetopia is another town where many bees live. In particular, Kuro will avoid any pair of towns $$$(u, v)$$$ if on the path from $$$u$$$ to $$$v$$$, he reaches Beetopia after he reached Flowrisa, since the bees will be attracted with the flower smell on Kuro’s body and sting him.

Kuro wants to know how many pair of city $$$(u, v)$$$ he can take as his route. Since he’s not really bright, he asked you to help him with this problem.

Input

The first line contains three integers $$$n$$$, $$$x$$$ and $$$y$$$ ($$$1 \leq n \leq 3 \cdot 10^5, 1 \leq x, y \leq n$$$, $$$x \ne y$$$) - the number of towns, index of the town Flowrisa and index of the town Beetopia, respectively.

$$$n - 1$$$ lines follow, each line contains two integers $$$a$$$ and $$$b$$$ ($$$1 \leq a, b \leq n$$$, $$$a \ne b$$$), describes a road connecting two towns $$$a$$$ and $$$b$$$.

It is guaranteed that from each town, we can reach every other town in the city using the given roads. That is, the given map of towns and roads is a tree.

Output

A single integer resembles the number of pair of towns $$$(u, v)$$$ that Kuro can use as his walking route.

Examples

Input

3 1 3
1 2
2 3

Output

5

Input

3 1 3
1 2
1 3

Output

4

Note

On the first example, Kuro can choose these pairs:

• $$$(1, 2)$$$: his route would be $$$1 \rightarrow 2$$$,
• $$$(2, 3)$$$: his route would be $$$2 \rightarrow 3$$$,
• $$$(3, 2)$$$: his route would be $$$3 \rightarrow 2$$$,
• $$$(2, 1)$$$: his route would be $$$2 \rightarrow 1$$$,
• $$$(3, 1)$$$: his route would be $$$3 \rightarrow 2 \rightarrow 1$$$.

Kuro can't choose pair $$$(1, 3)$$$ since his walking route would be $$$1 \rightarrow 2 \rightarrow 3$$$, in which Kuro visits town $$$1$$$ (Flowrisa) and then visits town $$$3$$$ (Beetopia), which is not allowed (note that pair $$$(3, 1)$$$ is still allowed because although Kuro visited Flowrisa and Beetopia, he did not visit them in that order).

On the second example, Kuro can choose the following pairs:

• $$$(1, 2)$$$: his route would be $$$1 \rightarrow 2$$$,
• $$$(2, 1)$$$: his route would be $$$2 \rightarrow 1$$$,
• $$$(3, 2)$$$: his route would be $$$3 \rightarrow 1 \rightarrow 2$$$,
• $$$(3, 1)$$$: his route would be $$$3 \rightarrow 1$$$.

【题意】

给一个$$$n$$$个点，$$$n$$$-1条路径的连通无向图（其实就是树），求不会先经过$$$x$$$再经过$$$y$$$的路径$$$(u, v)$$$的个数，其中$$$(u, v)$$$和$$$(v, u)$$$被视为不同的路径。

【分析】

由于是在树上的操作，从$$$u$$$ 到$$$v$$$的路径是被$$$u,v$$$唯一确定的，所以转而求端点对的个数。

总端点个数有3e5，但是需要检查的点只有2个，遍历所有路径并不划算，不如转而用排除法，总路径数 - 不符合的路径数 = 答案

总路径数很好算，只需要根据组合原理 = $$$A^2_n = n*(n-1)$$$。不符合的路径数可以这么求——把$$$x$$$到$$$y$$$的路径看成一个整体，其他部分看成挂在路径上的，分为：挂在$$$x$$$上的部分，挂在$$$y$$$上的部分，以及挂在这个路径其他点上的部分，把$$$x$$$与挂在$$$x$$$上的部分合称为为$$$x$$$部分，把$$$y$$$和$$$y$$$相连的部分合称为$$$y$$$部分。

一条先经过$$$x$$$再经过$$$y$$$的路径，必定起于与$$$x$$$部分，经过$$$x$$$到$$$y$$$的路径，最后止于与$$$y$$$部分。对于其他路径，起点不在$$$x$$$部分的，经过了$$$x$$$后就不会再经过$$$y$$$了，因为它一定是从$$$x->y$$$的路径的中部走到$$$x$$$的，在经过$$$x$$$后就不能再回头了；终点不在$$$y$$$部分的，自然不会经过y。

所以不符合的路径数=$$$x$$$部分的大小*$$$y$$$部分的大小

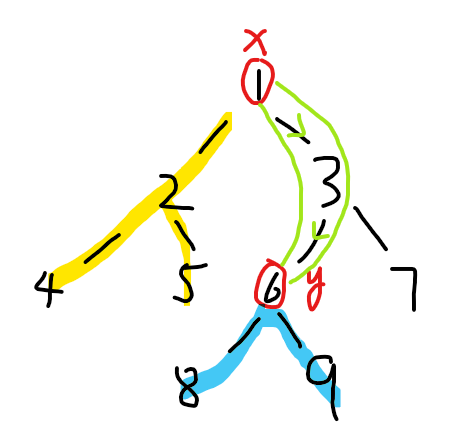
上个图演示一下：x是1，y是3，那么从$$$\{1,2,4,5\}$$$到$$$\{6,8,9\}$$$的路径都必须经过$$$1\to 3\to 6$$$，而只要起点不是$$$\{1,2,4,5\}$$$或者终点不是$$$\{6,8,9\}$$$的路径都是可以走的。所以答案是9*8 - 4*3 = 60。

【代码】

#include<stdio.h>
#include<vector>
using std::vector;
#define N_max 100005
typedef long long ll;
int x,y;
vector<int> node[300005];
ll ans, n, cnt[2] = { 0 };
int vis[300005];

//从x出发，搜索到y的路径并把经过的点全部标记为1
int findy(int cur) {
	if (cur != y) {
		vis[cur] = -1;
		int next;
		for (int t = 0; t < node[cur].size(); ++t) {
			next = node[cur][t];
			if (vis[next] != -1)
				if (1 == findy(next)) {
					vis[cur] = 1; return 1;
				}
		}
	}
	if (cur == y) {
		vis[cur] = 1; return 1;
	}
	return 0;//因为是连通图，一定能找到y，返回0是防止编译器检查到没有返回值
}

//搜索去掉x->y路径后，与x连通的点的个数
void calx(int cur) {
	if (vis[cur] == 2)return;
		vis[cur] = 2;
		cnt[0]++;
		int next;
		for (int t = 0; t < node[cur].size(); ++t) {
			next = node[cur][t];
			if (vis[next] != 1)
				calx(next);
				}
}
//搜索去掉x->y路径后，与y连通的点的个数
void caly(int cur) {
	if (vis[cur] == 2)return;
	vis[cur] = 2;
	cnt[1]++;
	int next;
	for (int t = 0; t < node[cur].size(); ++t) {
		next = node[cur][t];
		if (vis[next] != 1)
			caly(next);
	}
}

//上面的计数可以用一个函数实现的，比赛的时候写的比较无脑:(
int main() {
	int a1, a2;
	scanf("%lld %d %d", &n,&x,&y);
	for (int i = 0; i < n-1; ++i) {
		scanf("%d %d", &a1, &a2);
		node[a1].emplace_back(a2);
		node[a2].emplace_back(a1);
	}
	ans = n*(n - 1);
	findy(x);
	calx(x);
	caly(y);
	printf("%lld\n",ans-cnt[0]*cnt[1]);
}