水库抽样Reservoir Sampling（蓄水池问题）

知识复习

空间亚线性算法：由于大数据算法中涉及到的数据是海量的，数据难以放入内存计算，所以一种常用的处理办法是不对全部数据进行计算，而只向内存里放入小部分数据，仅使用内存中的小部分数据，就可以得到一个有质量保证的结果。

数据流算法：是指数据源源不断地到来，根据到来的数据返回相应的部分结果。适用于两种情况：第一、数据量非常大仅能扫描一次时，可以把数据看成数据流，把扫描看成数据到来。第二、数据更新非常快，不能把所有数据都保存下来再计算结果，此时可以把数据看成是一个数据流。

在一些情况下，空间亚线性算法也叫数据流算法。

水库抽样（海量数据随机抽样问题）（蓄水池问题）

输入：一组数据，其大小未知

输出：这组数据的k个均匀抽样

要求：
仅扫描数据一次。
空间复杂度为O(K)。空间复杂度与整个数据量无关，只与抽样大小有关。
扫描到数据的前n 个数据时（n>k）,保存当前已扫描数据的k个均匀抽样。

问题可以理解为：蓄水池（水库）的容量为k，对于n（n>k）个元素，如果第i个元素（i从1逐渐递增至n）以k/i的概率决定是否将它放入蓄水池，当i=n时，蓄水池中存放的是n个元素的均匀抽样，每个数字最终被存在数组中的概率相等，为k/n。见下面的证明

水库抽样算法描述

1、申请一个长度为k的数组A保存抽样。
2、保存首先接收到的k个元素
3、当接收到第i个新元素t时，以k/i的概率随机替换A中的元素(即生成[1,i]间随机数j，若j<=k，则以t替换A[j])

Init : a reservoir with the size： k

for i= k+1 to N

    M=random(1, i);

    if( M < k)

     SWAP the Mth value and ith value

end for

证明一

当接收到第i个新元素t时，以k/i的概率保存在水库中，所以在接收第i+1个数时，第i个数还能保存在水库当中的概率是1-1/(i+1)，因为在接收到第i+1个数时要以k/(i+1)的概率随机替换，而第i个数被选中的概率是1/k，它们相乘即为1/(i+1)。1/(i+1)为第i个元素被换出水库的概率，所以1-1/(i+1)就是在接收第i+1个元素时第i个元素在数组中的概率。同理，在接收第i+2个元素时，第i个元素让然保留在水库中的概率为1-1/(i+2)。以此类推，当接收第n个元素时，第i个元素保存在水库中的概率为1-1/n。只有这些事件都放生了，最终第i个元素才能保留在水库当中。因此第i个元素最终被保留在水库抽样当中的概率，就是这些事件的概率的乘积，即

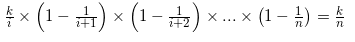
证明二

（1）第一步初始化。出现在水库中的前k个元素，直接保存在数组A中。前k个数被选中的概率都是一致的，都是1。

（2）第二步。在处理第k+1个元素时分两种情况：

情况1：第k+1个元素未被选中，数组中没有元素被替换；此时，数组中每个元素的出现概率肯定是一样的，这很显然。但具体是多少呢？就是第k+1个元素未被选中的概率：1-P(第k+1个元素被选中)=1-k/(k+1)=1/(k+1)。（由于第k+1个元素被选中的概率是k/(k+1)（根据公式k/i））

情况2：第k+1个元素被选中，数组中某个元素被第k+1个元素替换掉。第k+1个元素被选中的概率是k/(k+1)（根据公式k/i），所以这个新元素在水库中出现的概率就一定是k/(k+1)（不管它替换掉哪个元素）。下面来看水库中原有元素最终还能留在水库中的概率，水库中原有数据被替换的几率都相等为1/k。水库中任意一个元素被替换掉的概率是：(k/k+1)*(1/k)=1/(k+1)，意即首先要第k+1个元素被选中，然后该元素在k个元素中被选中。那它未被替换的概率就是1-1/(k+1)=k/(k+1)。可以看出来，旧元素和新元素出现的概率是相等的。

（3）第k+1之后面每个元素都重复第二步，即第i （i>k+1）个元素以k/i的概率决定是否将它放入蓄水池，最终所有元素出现在水库中的概率相等。

来源： https://blog.csdn.net/so_geili/article/details/52937212

来自为知笔记(Wiz)