PTA (Advanced Level) 1018 Public Bike Management

Public Bike Management

　　There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

　　The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfectcondition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.

　　When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

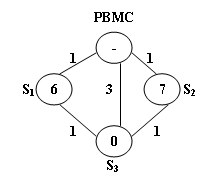
　　The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at S​3​​, we have 2 different shortest paths:

1. PBMC -> S​1​​ -> S​3​​. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from S​1​​ and then take 5 bikes to S​3​​, so that both stations will be in perfect conditions.

2. PBMC -> S​2​​ -> S​3​​. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.

Input Specification:

　　Each input file contains one test case. For each case, the first line contains 4 numbers: C​max​​ (≤), always an even number, is the maximum capacity of each station; N (≤), the total number of stations; S​p​​, the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and M, the number of roads. The second line contains N non-negative numbers C​i​​ (,) where each C​i​​ is the current number of bikes at S​i​​ respectively. Then Mlines follow, each contains 3 numbers: S​i​​, S​j​​, and T​ij​​ which describe the time T​ij​​ taken to move betwen stations S​i​​ and S​j​​. All the numbers in a line are separated by a space.

Output Specification:

　　For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0. Finally after another space, output the number of bikes that we must take back to PBMC after the condition of S​p​​ is adjusted to perfect.

　　Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge's data guarantee that such a path is unique.

Sample Input:

10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1

Sample Output:

3 0->2->3 0

解题思路：
　　本题题意是，杭州市有一些共享单车站，给出车站的最大容量（一定是偶数），给出车站数量与车站之间道路的信息，车站的最优状态为最大容量的一半。给定目标车站，控制中心现在要携带或从路过的其他车站取出一些自行车，使路程中路过的所有车站和目标车站都变为最优状态，多的自行车将被带回控制中心。要求计算并输出最短路径和最短路径情况下的携带数与带回数，如果有多条最短路径那么选择携带数最少的一条，如果还有是多条路径，那么选择带回数最少的一条。（到达目标车站后之间带着多余的自行车之间传送回控制中心，不在经过任何车站）。

　　输入信息：第一行给出4个整数，分别为 最大容量Cmax ，车站数量n， 目标车站sp，道路数量m，下一行给出n个整数代表每个车站当前自行车数量，之后跟随m行，每行3个整数，分别为，道路连接的两个车站和道路长度。

　　车站的范围为1 ~ n，0为控制中心。

　　可以先用迪杰斯特拉获得所有最短路径。之后搜索所有最短路径获得携带数（携带数相同获得最小的带回数）最小的路径，按要求输出。

　　利用Dijkstra建立一颗最短路径树

void Dijkstra(int st){  //传入起点，这里之间传入0控制中心即可
    dis[st] = ;    //dis储存控制中心到所有车站的最短距离
    //控制中心到自己的最短距离为0
    for(int i = ; i <= n; i++){    //获取没有访问过的车站中距离控制中心最近的车站
        int u = -, minLength = INT_MAX;
        //u记录最近的车站， minLength记录最短距离
        for(int j = ; j <= n; j++){
            //vis记录车站是否已经访问
            if(dis[j] < minLength && !vis[j]){
                u = j;
                minLength = dis[j];
            }
        }
        if(u == -) //如果u还是-1表示其他车站和控制中心不连通
            return;
        vis[u] = true;  //将最近的车站标记为已访问
        for(int j = ; j <= n; j++){    //遍历所有结点用u车站优化控制中心与其他未访问车站的距离
            if(!vis[j] && G[u][j] != INT_MAX){  //j车站未访问且与u车站之间有道路
                if(dis[j] > dis[u] + G[u][j]){  //判断是否能优化
                    dis[j] = dis[u] + G[u][j];  //如果能优化
                    pre[j].clear(); //j车站的前驱车站清空并重新记录为u
                    pre[j].push_back(u);
                }else if(dis[j] == dis[u] + G[u][j]){
                    //若不能优化但是以u为中转是j车站到控制中心的距离和dis数组中记录的 j车站到控制中心的距离相等
                    //j车站的前驱增加u
                    pre[j].push_back(u);
                }
            }
        }
    }
}

　　之后深搜遍历最短路径树获得携带数最少（如果仍有多条道路则获得带回数最少）的路线。

void DFS(int v){
    if(v == ){ //这里我们逆序遍历路径，从终点车站开始到控制中心0为止
        //应为最短路径树中记录控制0为叶子结点，目标车站sp为根结点
        path.push_back();
        judge();    //判断当前路径的携带数与带回树是否可以优化答案
        path.pop_back();
        return;
    }
    path.push_back(v);
    for(auto i : pre[v]){
        DFS(i);
    }
    path.pop_back();
}

　　由于DFS中我们时倒序遍历的最短路径，所以在判断每条路径是否可以优化答案时，要先将DFS中获取的路径反转，之后遍历这条路径获得其携带数与带回数即可。

void judge(){
    int need = , backn = ;    //need记录携带数 backn记录带回数
    int half = Cmax / ;    //half记录最优状态车站中车辆数
    reverse(path.begin(), path.end());
    bool flag = false;  //道路开始位置为控制中心0，我们不需要将控制中心的车辆数调整为最优状态
    //所以我们用flag = false表示正在访问控制中心
    for(auto i : path){
        if(!flag){  //跳过控制中心
            flag = true;
            continue;
        }
        if(spValue[i] > half){  //当前车站中的共享单车数量大于最优状态数量
            backn += spValue[i] - half; //将多出的车辆带走
        }else{
            if(backn > half - spValue[i])   //如果当前携带的车辆足以将该车站补充为最优状态
                backn -= half - spValue[i]; //当前携带数减去缺少车辆数
            else{
                need += (half - spValue[i]) - backn;
                //如果不足以补足当前车站就将所有携带车辆放入该车站，之后还是不足的车辆从控制中心携带
                backn = ;
            }
        }
    }
    if(need < minNeed){ //比较答案与当前路径的携带数
        minNeed = need;
        minBack = backn;
        ansPath = path;
    }else if(need == minNeed && backn < minBack){   //携带数一致比较带回数
        minBack = backn;
        ansPath = path;
    }
    reverse(path.begin(), path.end());  //为了继续DFS重新将路径反转
}

　　AC代码

 #include <bits/stdc++.h>
 using namespace std;
 const int maxn = ;
 int n, m, Cmax, sp; //n记录车站数量， m记录道路数量， Cmax记录车站最大容量（Cmax/2就是车站最优数量）
 int G[maxn][maxn];  //G储存车站之间的邻接矩阵
 int spValue[maxn], dis[maxn];   //spValue记录每个车站当前的车辆数， dis记录每个车站到控制中心的最短距离
 bool vis[maxn] = {false};   //vis用于在寻找最短路径时判断车站是否已经访问
 int minNeed, minBack;
 vector<int> path, ansPath, pre[maxn];
 void Dijkstra(int st){  //传入起点，这里之间传入0控制中心即可
     dis[st] = ;    //dis储存控制中心到所有车站的最短距离
     //控制中心到自己的最短距离为0
     for(int i = ; i <= n; i++){    //获取没有访问过的车站中距离控制中心最近的车站
         int u = -, minLength = INT_MAX;
         //u记录最近的车站， minLength记录最短距离
         for(int j = ; j <= n; j++){
             //vis记录车站是否已经访问
             if(dis[j] < minLength && !vis[j]){
                 u = j;
                 minLength = dis[j];
             }
         }
         if(u == -) //如果u还是-1表示其他车站和控制中心不连通
             return;
         vis[u] = true;  //将最近的车站标记为已访问
         for(int j = ; j <= n; j++){    //遍历所有结点用u车站优化控制中心与其他未访问车站的距离
             if(!vis[j] && G[u][j] != INT_MAX){  //j车站未访问且与u车站之间有道路
                 if(dis[j] > dis[u] + G[u][j]){  //判断是否能优化
                     dis[j] = dis[u] + G[u][j];  //如果能优化
                     pre[j].clear(); //j车站的前驱车站清空并重新记录为u
                     pre[j].push_back(u);
                 }else if(dis[j] == dis[u] + G[u][j]){
                     //若不能优化但是以u为中转是j车站到控制中心的距离和dis数组中记录的 j车站到控制中心的距离相等
                     //j车站的前驱增加u
                     pre[j].push_back(u);
                 }
             }
         }
     }
 }
 void judge(){
     int need = , backn = ;    //need记录携带数 backn记录带回数
     int half = Cmax / ;    //half记录最优状态车站中车辆数
     reverse(path.begin(), path.end());
     bool flag = false;  //道路开始位置为控制中心0，我们不需要将控制中心的车辆数调整为最优状态
     //所以我们用flag = false表示正在访问控制中心
     for(auto i : path){
         if(!flag){  //跳过控制中心
             flag = true;
             continue;
         }
         if(spValue[i] > half){  //当前车站中的共享单车数量大于最优状态数量
             backn += spValue[i] - half; //将多出的车辆带走
         }else{
             if(backn > half - spValue[i])   //如果当前携带的车辆足以将该车站补充为最优状态
                 backn -= half - spValue[i]; //当前携带数减去缺少车辆数
             else{
                 need += (half - spValue[i]) - backn;
                 //如果不足以补足当前车站就将所有携带车辆放入该车站，之后还是不足的车辆从控制中心携带
                 backn = ;
             }
         }
     }
     if(need < minNeed){ //比较答案与当前路径的携带数
         minNeed = need;
         minBack = backn;
         ansPath = path;
     }else if(need == minNeed && backn < minBack){   //携带数一致比较带回数
         minBack = backn;
         ansPath = path;
     }
     reverse(path.begin(), path.end());  //为了继续DFS重新将路径反转
 }
 void DFS(int v){
     if(v == ){ //这里我们逆序遍历路径，从终点车站开始到控制中心0为止
         //应为最短路径树中记录控制0为叶子结点，目标车站sp为根结点
         path.push_back();
         judge();    //判断当前路径的携带数与带回树是否可以优化答案
         path.pop_back();
         return;
     }
     path.push_back(v);
     for(auto i : pre[v]){
         DFS(i);
     }
     path.pop_back();
 }
 int main()
 {
     while(scanf("%d%d%d%d", &Cmax, &n, &sp, &m) != EOF){    //输入最大容量 车站数量 目标车站 道路数量
         fill(G[], G[] + maxn * maxn, INT_MAX);    //将所有车站之间设为不可达
         for(int i = ; i < maxn; i++){
             pre[i].clear(); //清空最短路径树
         }
         path.clear();   //清空用来记录每个路径的容器
         ansPath.clear();    //清空用来记录答案路径的容器
         for(int i = ; i <= n; i++){
             scanf("%d", &spValue[i]);   //输入每个车站当前的车辆数
         }
         for(int i = ; i < m; i++){ //输入路径
             int u, v;
             scanf("%d%d", &u, &v);
             scanf("%d", &G[u][v]);
             G[v][u] = G[u][v];  //双向路径
         }
         memset(vis, false, sizeof(vis));    //将所有车站设为未访问
         fill(dis, dis + maxn, INT_MAX); //所有车站到控制中心的距离为无穷大
         Dijkstra();    //迪杰斯特拉获取最短路径树
         minNeed = INT_MAX, minBack = INT_MAX;   //记录答案携带数与带回数为无穷多
         DFS(sp);    //深搜最短路径树获取答案
         printf("%d ", minNeed); //输出携带数
         bool flag = false;
         for(auto i : ansPath){  //输出路径
             if(flag)
                 printf("->");
             printf("%d", i);
             flag = true;
         }
         printf(" %d\n", minBack);   //输出带回数
     }
     return ;
 }