ROC曲线【转】

受试者工作特征曲线（receiver operating characteristic curve, 简称ROC曲线），又称为感受性曲线（sensitivity curve）。得此名的原因在于曲线上各点反应着相同的感受性，它们都是对同一信号刺激的反应，只不过是在几种不同的判定标准下所得的结果而已。接受者操作特性曲线就是以虚拟概率为横轴，击中概率为纵轴所成的坐标图，和被试在特定刺激条件下由于采用不同的判断标准得出的不同结果画出的曲线。

概念：ROC曲线是根据一系列不同的二分类方式（分界值或决定域），以真阳性率（灵敏度）为纵坐标

ROC曲线的例子

　　考虑一个二分问题，即将实例分成正类（positive）或负类（negative）。对一个二分问题来说，会出现四种情况。如果一个实例是正类并且也被 预测成正类，即为真正类（True positive）,如果实例是负类被预测成正类，称之为假正类（False positive）。相应地，如果实例是负类被预测成负类，称之为真负类（True negative）,正类被预测成负类则为假负类（false negative）。

TP：正确肯定的数目；

FN：漏报，没有正确找到的匹配的数目；

FP：误报，给出的匹配是不正确的；

TN：正确拒绝的非匹配对数；

 

　　列联表如下表所示，1代表正类，0代表负类。

 

　　

		预测
		1	0	合计
实际	1	True Positive（TP）	False Negative（FN）	Actual Positive(TP+FN)
	0	False Positive（FP)	True Negative(TN)	Actual Negative(FP+TN)
合计		Predicted Positive(TP+FP)	Predicted Negative(FN+TN)	TP+FP+FN+TN

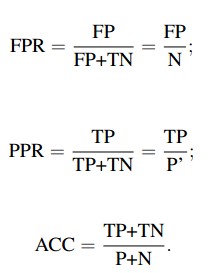
从列联表引入两个新名词。其一是真正类率(true positive rate ,TPR), 计算公式为TPR=TP/ (TP+ FN)，刻画的是分类器所识别出的 正实例占所有正实例的比例。另外一个是负正类率(false positive rate, FPR),计算公式为FPR= FP / (FP + TN)，计算的是分类器错认为正类的负实例占所有负实例的比例。还有一个真负类率（True Negative Rate，TNR），也称为specificity,计算公式为TNR=TN/ (FP+ TN) = 1-FPR。

其中，两列True matches和True non-match分别代表应该匹配上和不应该匹配上的

两行Pred matches和Pred non-match分别代表预测匹配上和预测不匹配上的

 

　　在一个二分类模型中，对于所得到的连续结果，假设已确定一个阀值，比如说 0.6，大于这个值的实例划归为正类，小于这个值则划到负类中。如果减小阀值，减到0.5，固然能识别出更多的正类，也就是提高了识别出的正例占所有正例 的比类，即TPR,但同时也将更多的负实例当作了正实例，即提高了FPR。为了形象化这一变化，在此引入ROC，ROC曲线可以用于评价一个分类器。

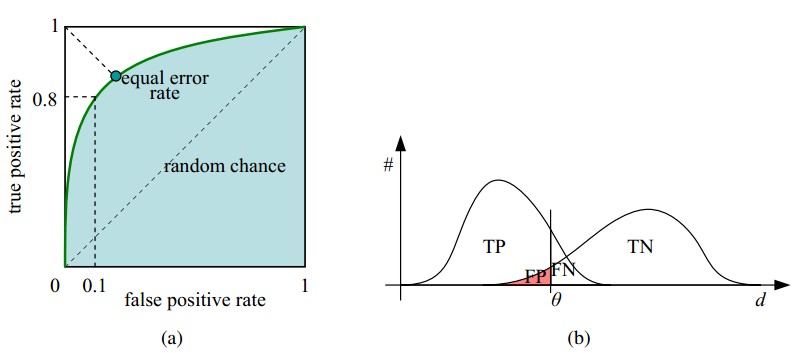
ROC曲线和它相关的比率

(a)理想情况下，TPR应该接近1，FPR应该接近0。

ROC曲线上的每一个点对应于一个threshold，对于一个分类器，每个threshold下会有一个TPR和FPR。

比如Threshold最大时，TP=FP=0，对应于原点；Threshold最小时，TN=FN=0，对应于右上角的点(1,1)

(b)P和N得分不作为特征间距离d的一个函数，随着阈值theta增加，TP和FP都增加

 

　　Receiver Operating Characteristic,翻译为"接受者操作特性曲线"，够拗口的。曲线由两个变量1-specificity 和 Sensitivity绘制. 1-specificity=FPR，即负正类率。Sensitivity即是真正类率，TPR(True positive rate),反映了正类覆盖程度。这个组合以1-specificity对sensitivity,即是以代价(costs)对收益(benefits)。

此外，ROC曲线还可以用来计算“均值平均精度”（mean average precision），这是当你通过改变阈值来选择最好的结果时所得到的平均精度（PPV）.

 

　　下表是一个逻辑回归得到的结果。将得到的实数值按大到小划分成10个个数 相同的部分。

 

　　

Percentile	实例数	正例数	1-特异度(%)	敏感度(%)
10	6180	4879	2.73	34.64
20	6180	2804	9.80	54.55
30	6180	2165	18.22	69.92
40	6180	1506	28.01	80.62
50	6180	987	38.90	87.62
60	6180	529	50.74	91.38
70	6180	365	62.93	93.97
80	6180	294	75.26	96.06
90	6180	297	87.59	98.17
100	6177	258	100.00	100.00

其正例数为此部分里实际的正类数。也就是说，将逻辑回归得到的结 果按从大到小排列，倘若以前10%的数值作为阀值，即将前10%的实例都划归为正类，6180个。其中，正确的个数为4879个，占所有正类的 4879/14084*100%=34.64%，即敏感度；另外，有6180-4879=1301个负实例被错划为正类，占所有负类的1301 /47713*100%=2.73%,即1-特异度。以这两组值分别作为x值和y值，在excel中作散点图。，假阳性率（1-特异度）为横坐标绘制的曲线。

转自 http://blog.csdn.net/abcjennifer/article/details/7359370