ZOJ3466-The Hive II

题意

有一个六边形格子，共 \(n\) 行，每行有 8 个位置，有一些格子不能走。求用一些环覆盖所有可走格子的方案数。\(n\le 10\) 。

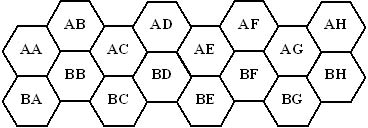
分析

插头dp，只不过是六边形上的，分奇数列和偶数列讨论，转移不太一样，但大同小异。编号需要插空，注意以下就行了。复杂度为 \(O(nm2^{2m})\) 。

代码

cc_hash_table 多次用实力证明，他跑得比其他任何内置的 hash_map 都快！

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
typedef long long giant;
typedef cc_hash_table<int,giant> Map;
typedef Map::iterator itt;
const int maxn=11;
const int m=8,maxm=m+1;
int n,q;
bool no[maxn][maxm];
Map f,g;
inline int get(int x,int p) {return (x>>p)&1;}
inline int mod(int x,int p,int d) {return (x&(~(1<<p)))+(d<<p);}
inline int mor(int x,int p,int d) {
	int bef=x&((1<<p)-1);
	return ((x-bef)<<d)+bef;
}
inline int mol(int x,int p,int d) { // cover the pth
	int bef=x&((1<<p)-1);
	return (((x-bef)>>(p+2))<<p)+bef;
}
int work() {
	memset(no,0,sizeof no);
	while (q--) {
		static char s[5];
		scanf("%s",s);
		no[s[0]-'A'+1][s[1]-'A'+1]=true;
	}
	f.clear(),g.clear();
	f[0]=1;
	for (int i=1;i<=n;++i) {
		f.swap(g),f.clear();
		for (itt it=g.begin();it!=g.end();++it) {
			const int &d=it->first;
			const giant &w=it->second;
			if (get(d,1)==0 && get(d,17)==0) f[d]=w;
		}
		for (int j=1;j<=m;++j) {
			f.swap(g),f.clear();
			for (itt it=g.begin();it!=g.end();++it) {
				const int &d=it->first;
				const giant &w=it->second;
				if (j&1) {
					int a=j*2-1,t=mor(d,a+2,2),x=get(d,a),y=get(d,a+1),sum=x+y;
					if (no[i][j]) {
						if (!sum) f[t]+=w;
						continue;
					}
					if (!sum) {
						for (int k=0;k<4;++k) for (int r=k+1;r<4;++r) f[mod(mod(t,a+k,1),a+r,1)]+=w;
					} else {
						int v=mod(mod(t,a,0),a+1,0);
						if (sum==1) for (int k=0;k<4;++k) f[mod(v,a+k,1)]+=w; else
						if (sum==2) f[v]+=w;
					}
				} else {
					int a=j<<1,t=mol(d,a+2,2),u=get(d,a),x=get(d,a+1),y=get(d,a+2),z=get(d,a+3),sum=u+x+y+z;
					if (no[i][j]) {
						if (!sum) f[t]+=w;
						continue;
					}
					if (!sum) f[mod(mod(t,a,1),a+1,1)]+=w; else {
						int v=mod(mod(t,a,0),a+1,0);
						if (sum==1) for (int k=0;k<2;++k) f[mod(v,a+k,1)]+=w; else
						if (sum==2) f[v]+=w;
					}
				}
			}
		}
	}
	printf("%lld\n",f[0]);
}
int main() {
#ifndef ONLINE_JUDGE
	freopen("test.in","r",stdin);
#endif
	while (~scanf("%d%d",&n,&q)) work();
	return 0;
}