与数论的厮守02:整数的因子分解—Pollard_Rho

　　学Pollard_Rho之前，你需要学会：Miller Rabin。

　　这是一个很高效的玄学算法，用来对大整数进行因数分解。

　　我们来分解n。若n是一个素数，那么就不需要分解了。所以我们还得能够判断一个数是否为素数才行。而n是个大整数，显然普通的试除法和筛法都是不够它跑的。所以我们就得考虑用Miller Rabin来判断。

　　但n不是素数呢？这就得用Pollard_Rho了。首先我们来看一个有趣的东西：生日悖论。

　　生日悖论：说简单点，就是在N个数里面选k个，当k接近√N时，选出两个相同数的几率约为50%。比如，不考虑闰年时，一个班若有23个人，则有两人生日相同的概率约为50%；但人数达到60时，概率约为基本上就是100%了，这严重违背了我们的生活经验，所以被列为了悖论。

　　模仿着生日悖论，若在1~N里面选k个数X₁,X₂...X_K,若k足够大，则很大几率有gcd(X_i-X_j，N)>1，也就是二者不互质，此时gcd(X_i-X_j，N)就是N的一个因数了。但是这样做复杂度又退回了O(k²)，处理不好还能退化为O(n²)。所以Pollard_Rho是有改进的。首先是空间。改进的Pollard_Rho只需要存相邻的两个数：X_i，X_i+1。同时为了得到这些数，Pollard_Rho还设计了一个函数：f(X_i)=(X_i²+c) mod n。这个c可以rand出来。然后再计算d=gcd(|X_i-X_i+1|，N)，若d>1，则递归分解d和n/d。

　　但是mod n的值∈[0,n-1]之间，只有n个数，所以当递归够深时就会出现循环，这不利于我们的算法。就是这个样子(图是盗的)：

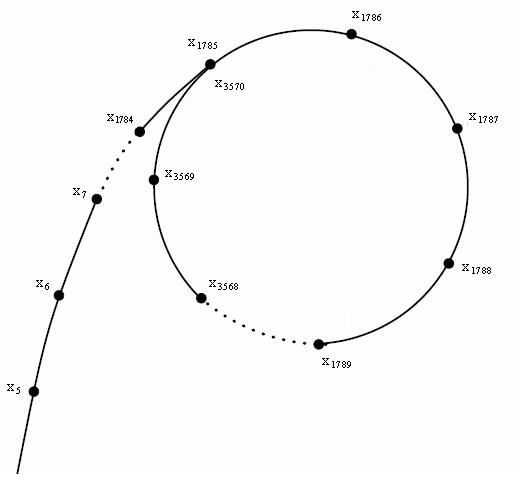
　　这里就有一个优化。像刚才的图一样，我们可以把循环节看成是一个环，我们只需要找出环就可以停下了。不然就一直跑到递归的数为素数为止。怎么找环呢？我们会想一下小学的追及问题。假设跑道上有两个人，一个高个子和一个矮个子。矮个子的速度为1，高个子的速度为2。如果跑道是无限长的直线，那高个子就会永远跑在矮个子前面。但如果有环，那么高个子就肯定追得到矮个子。Pollard_Rho就可以用这个办法来找环。

(这个图也是盗的)