[bzoj1018][SHOI2008]堵塞的交通traffic_线段树

bzoj-1018 SHOI-2008 堵塞的交通traffic

参考博客：https://www.cnblogs.com/MashiroSky/p/5973686.html

题目大意：有一天，由于某种穿越现象作用，你来到了传说中的小人国。小人国的布局非常奇特，整个国家的交通系统可以被看成是一个2行C列的矩形网格，网格上的每个点代表一个城市，相邻的城市之间有一条道路，所以总共有2C个城市和3C-2条道路。 小人国的交通状况非常槽糕。有的时候由于交通堵塞，两座城市之间的道路会变得不连通，直到拥堵解决，道路才会恢复畅通。初来咋到的你决心毛遂自荐到交通部某份差事，部长听说你来自一个科技高度发达的世界，喜出望外地要求你编写一个查询应答系统，以挽救已经病入膏肓的小人国交通系统。 小人国的交通部将提供一些交通信息给你，你的任务是根据当前的交通情况回答查询的问题。交通信息可以分为以下几种格式：

　　Close r1 c1 r2 c2：相邻的两座城市(r1,c1)和(r2,c2)之间的道路被堵塞了；

　　Open r1 c1 r2 c2：相邻的两座城市(r1,c1)和(r2,c2)之间的道路被疏通了；

　　Ask r1 c1 r2 c2：询问城市(r1,c1)和(r2,c2)是否连通。如果存在一条路径使得这两条城市连通，则返回Y，否则返回N；

数据范围：$0\le C\le 10^5$，$1\le Number_{message} \le 10^5$。

---

想法：

哇哦。。。

这题真的能想出来？

我们用线段树维护一个列在$(l,r)$之间的这么$r-l+1$个方格的连通性。

维护的信息如下图：

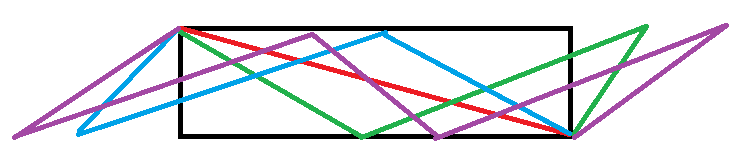
然后如果在同一行的话同理。

现在，假设从左到右，从上到下，矩阵的四个角依次命名为$s1$，$s2$，$s3$，$s4$。

我们就维护

$U$：第一行的$mid$和$mid+1$是否连通。

$D$：第二行的$mid$和$mid+1$是否连通。

$l$：$s1$和$s3$是否连通。

$r$：$s2$和$s4$是否连通。

$u$：$s1$和$s2$是否连通。

$d$：$s3$和$s4$是否连通。

$q$：$s1$和$s4$是否连通。

$p$：$s2$和$s3$是否连通。

之后暴力维护就好了。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ls p<<1
#define rs p<<1|1
#define N 100010
using namespace std;
struct Node
{
	bool U,D,l,r,u,d,p,q;
}a[N<<2];
inline void pushup(Node &p,Node l,Node r)
{
	p.l = l.l | (l.u & p.U & r.l & p.D & l.d);
	p.r = r.r | (r.u & p.U & l.r & p.D & r.d);
	p.u = (l.u & p.U & r.u) | (l.q & p.D & r.p);
	p.d = (l.d & p.D & r.d) | (l.p & p.U & r.q);
	p.q = (l.u & p.U & r.q) | (l.q & p.D & r.d);
	p.p = (l.d & p.D & r.p) | (l.p & p.U & r.u);
}
void build(int l,int r,int p)
{
	if(l==r) {a[p].U=a[p].D=a[p].u=a[p].d=true; return;}
	int mid=(l+r)>>1;
	build(l,mid,ls);
	build(mid+1,r,rs);
	pushup(a[p],a[ls],a[rs]);
}
void update_r(int x,int val,int opt,int l,int r,int p)
{
	int mid=(l+r)>>1;
	if(x==mid)
	{
		if(opt==1) a[p].U=val;
		else a[p].D=val;
		pushup(a[p],a[ls],a[rs]);
		return;
	}
	if(x<=mid) update_r(x,val,opt,l,mid,ls);
	else update_r(x,val,opt,mid+1,r,rs);
	pushup(a[p],a[ls],a[rs]);
}
void update_c(int x,int val,int l,int r,int p)
{
	if(l==r) {a[p].l=a[p].r=a[p].p=a[p].q=val; return;}
	int mid=(l+r)>>1;
	if(x<=mid) update_c(x,val,l,mid,ls);
	else update_c(x,val,mid+1,r,rs);
	pushup(a[p],a[ls],a[rs]);
}
Node query(int x,int y,int l,int r,int p)
{
	if(x<=l && r<=y) return a[p];
	int mid=(l+r)>>1;
	if(y<=mid) return query(x,y,l,mid,ls);
	else if(x>mid) return query(x,y,mid+1,r,rs);
	else
	{
		Node re=a[p];
		pushup(re,query(x,y,l,mid,ls),query(x,y,mid+1,r,rs));
		return re;
	}
}
int main()
{
	int c; cin >> c ;
	build(1,c,1);
	char s[10];
	int r1,r2,c1,c2;
	while(scanf("%s",s) != EOF)
	{
		if(s[0] == 'E') break;
		scanf("%d%d%d%d",&r1,&c1,&r2,&c2);
		if(c1 > c2) swap(c1,c2),swap(r1,r2);
		if(s[0] == 'O')
		{
			if(r1 == r2) update_r(c1,1,r1,1,c,1);
			else update_c(c1,1,1,c,1);
		}
		if(s[0] == 'C')
		{
			if(r1 == r2) update_r(c1,0,r1,1,c,1);
			else update_c(c1,0,1,c,1);
		}
		if(s[0] == 'A')
		{
			Node l = query(1,c1,1,c,1),x = query(c1,c2,1,c,1),r = query(c1,c,1,c,1);
			int ans;
			// printf("%d\n",x.u ? 1 : 0);
            // printf("%d\n",l.r ? 1 : 0);
            // printf("%d\n",x.p ? 1 : 0);
            // printf("%d\n",x.q ? 1 : 0);
            // printf("%d\n",r.l ? 1 : 0);
            // printf("%d\n",l.r ? 1 : 0);
            // printf("%d\n",x.d ? 1 : 0);
            // printf("%d\n",r.l ? 1 : 0);
			if(r1==1 && r2==1)
				/* puts("1"), */ans = x.u | (l.r & x.p) | (r.l & x.q) | (l.r & x.d & r.l);
			if(r1==1 && r2==2)
				/* puts("2"), */ans = x.q | (l.r & x.d) | (r.l & x.u) | (l.r & x.p & r.l);
			if(r1==2 && r2==1)
				/* puts("3"), */ans = x.p | (l.r & x.u) | (r.l & x.d) | (l.r & x.q & r.l);
			if(r1==2 && r2==2)
				/* puts("4"), */ans = x.d | (l.r & x.q) | (r.l & x.p) | (l.r & x.u & r.l);
			puts(ans ? "Y" : "N");
		}
	}
	return 0;
}

小结：妈的神仙题.....