LightOJ1234 Harmonic Number 调和级数求和

【题目】

【预备知识】

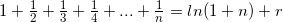，其中r是欧拉常数，const double r= 0.57721566490153286060651209;

这个等式在n很大 的时候 比较精确。

【解法】可以在 n较小的时候，比如n<1e6时，直接用预处理的打表O（1）求值，在n比较 大的时候，运用以上公式，此时要减去 1/（2*n）加以修正。

#include<iostream>
#include<cmath>
using namespace std;
const double euler= 0.57721566490153286060651209;
const int maxn = 1e6;
double a[maxn];
int cas = ;
int main(){
    long long n;
    a[] = ;
    for(int i=; i<maxn; i++){
        a[i] = a[i-] + 1.0 / i;
    }
    int t;
    cin>>t;
    while(t--){
        cin>>n;
        if(n < maxn){
            printf("Case %d: %.10lf\n",cas++,a[n]);
            continue;
        }
        double ans = log(+n) + euler - 1.0/(*n);
        printf("Case %d: %.10lf\n",cas++,ans);
    }
    return ;
} 

【分块打表】

虽然1e8的表打不出来，但1e6的表很好打，所以每隔100个数记录一次前缀和。到时用的时候，O（1）取出最接近n的前缀和，余下不足100个数暴力 求和即可。

#include<iostream>
#include<cmath>
using namespace std;
const double euler= 0.57721566490153286060651209;
const int maxn = 1e8+;

double a[maxn/];
int count = ;

int cas = ;
int main(){
    long long n;
    a[] = ;
    double s = ;
    for(int i=; i<maxn; i++){
        s += 1.0/i;
        if( i %  == ){
            a[count++] = s;
        }
    }
    int t;
    cin>>t;
    while(t--){
        double ans = ;
        cin>>n;
        int num = n / ;//对应a[num]
        ans += a[num];
         for(long long i=num *  + ; i<=n; i++){
             ans += 1.0/i;
         }
         printf("Case %d: %.10lf\n", cas++, ans);

    }
    return ;
}