洛谷 P1351 联合权值

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007 取余。

输入输出样例

输入样例#1：

5
1 2
2 3
3 4
4 5
1 5 2 3 10 

输出样例#1：

20 74

说明

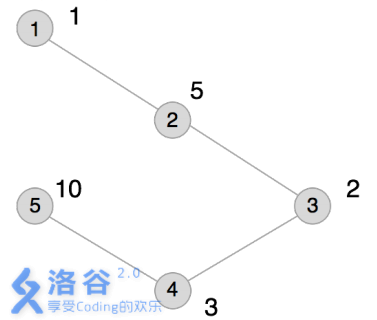
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

#include <cstdio>
#define zhx 10007
#define N 200000
int x[N+],y[N+],w[N+],c[N+],b[N+],ans1,ans2,n;
int max(int a,int b)
{
    return a>b?a:b;
}
int main()
{
    scanf("%d",&n);
    for(int i=;i<n;i++) scanf("%d%d",&x[i],&y[i]);
    for(int i=;i<=n;i++) scanf("%d",&w[i]);
    for(int i=;i<n;i++)
    {
        ans2=(ans2+w[x[i]]*b[y[i]]+w[y[i]]*b[x[i]])%zhx;
        b[x[i]]=(b[x[i]]+w[y[i]])%zhx;
        b[y[i]]=(b[y[i]]+w[x[i]])%zhx;
        ans1=max(ans1,max(w[x[i]]*c[y[i]],w[y[i]]*c[x[i]]));
        if(w[x[i]]>c[y[i]]) c[y[i]]=w[x[i]];
        if(w[y[i]]>c[x[i]]) c[x[i]]=w[y[i]];
    }
    printf("%d %d\n",ans1,ans2*%zhx);
    return ;
}