Generation I

Generation I

Oak is given N empty and non-repeatable sets which are numbered from 1 to N.

Now Oak is going to do N operations. In the i-th operation, he will insert an integer x between 1 and M to every set indexed between i and N.

Oak wonders how many different results he can make after the N operations. Two results are different if and only if there exists a set in one result different from the set with the same index in another result.

Please help Oak calculate the answer. As the answer can be extremely large, output it modulo 998244353.

输入描述:

The input starts with one line containing exactly one integer T which is the number of test cases. (1 ≤ T ≤ 20)

Each test case contains one line with two integers N and M indicating the number of sets and the range of integers. 
(1 ≤ N ≤ 1018, 1 ≤ M ≤ 1018, )

输出描述:

For each test case, output "Case #x: y" in one line (without quotes), where x is the test case number (starting from 1) and y is the number of different results 
modulo 998244353.

输入

2
2 2
3 4

输出

Case #1: 4
Case #2: 52

---

题意：有n个集合，n次操作，第i次操作中可以选一个数（数的范围是1~m），向i~n集合中都加入这个数，问最后有多少种不同的结果。

显然这题是因为集合不能有相同数的性质才导致答案不是m^n。

考虑全部的集合总共用了多少种不同的数，设共用了k种不同的数，则第一个集合有k种放法，由于每种操作对⼀个后缀有影响，区分⽅方案只要考虑第⼀个被影响的位置即可。

所以考虑剩下的n-1个集合的情况，则需要在其中选择k-1个集合放新的不同的数。最后就是不同的数的放入顺序不同也会导致答案不同，因此还要对k-1个数求一下排序数。

化简前的公式：

化简后的公式：

 

但是这题还一个比较坑的地方是n，m，mod都很大，lucas用不了，不能直接求组合数。

于是按照公式中的枚举变量k一步一步的来，先算k=1的情况，然后k=x的情况都可以由k=x-1的情况递推而来。

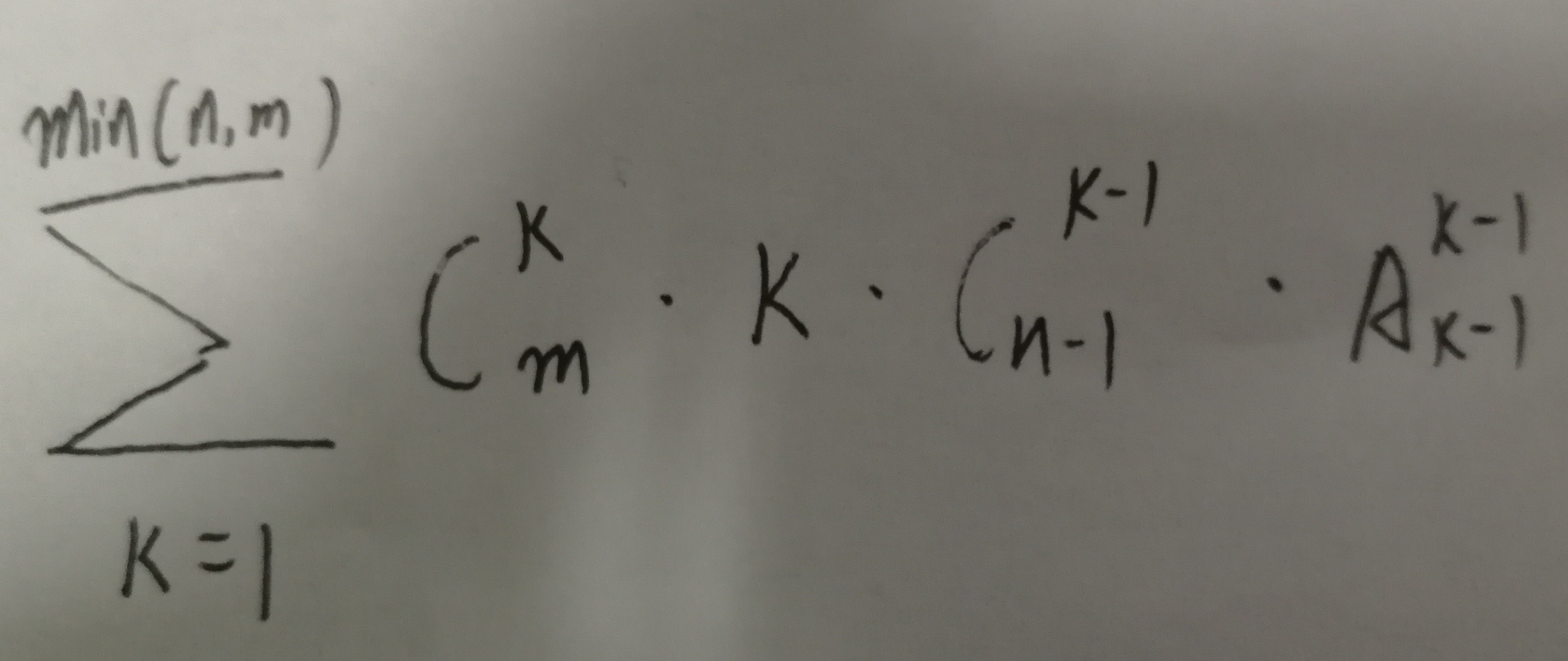
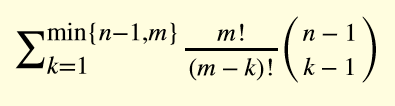
#include <iostream>
#define N 1000005
using namespace std;
const long long mod=;
long long ny[N+];
long long f(long long a,long long b)
{
    long long ans=;
    while(b>)
    {
        if(b%==)ans=(ans*a)%mod;

        b/=;
        a=(a*a)%mod;
    }
    return ans;
}

int main()
{
    int t,tot=;
    scanf("%d",&t);
    for(int i=;i<=N;i++)ny[i]=f(i,mod-);

    while(t--)
    {
        long long n,m,ans,upper,last;
        scanf("%lld %lld",&n,&m);

        upper=min(n,m);
        ans=last=m%mod;

        for(int i=;i<=upper;i++)
        {
            last*=(m+-i)%mod;
            last%=mod;
            last*=ny[i-];
            last%=mod;
            last*=(n+-i)%mod;
            last%=mod;
            ans+=last;
            ans%=mod;
        }

        printf("Case #%d: %lld\n",++tot,ans);
    }
    return ;
}