bzoj 1787 && bzoj 1832: [Ahoi2008]Meet 紧急集合（倍增LCA）算法竞赛进阶指南

题目描述

原题连接

Y岛风景美丽宜人，气候温和，物产丰富。

Y岛上有N个城市（编号\(1,2,…,N\)），有\(N-1\)条城市间的道路连接着它们。

每一条道路都连接某两个城市。

幸运的是，小可可通过这些道路可以走遍Y岛的所有城市。

神奇的是，乘车经过每条道路所需要的费用都是一样的。

小可可，小卡卡和小YY经常想聚会，每次聚会，他们都会选择一个城市，使得3个人到达这个城市的总费用最小。

由于他们计划中还会有很多次聚会，每次都选择一个地点是很烦人的事情，所以他们决定把这件事情交给你来完成。

他们会提供给你地图以及若干次聚会前他们所处的位置，希望你为他们的每一次聚会选择一个合适的地点。

输入格式

第一行两个正整数，\(N\)和\(M\)，分别表示城市个数和聚会次数。

后面有\(N-1\)行，每行用两个正整数\(A\)和\(B\)表示编号为\(A\)和编号为\(B\)的城市之间有一条路。

再后面有\(M\)行，每行用三个正整数表示一次聚会的情况：小可可所在的城市编号，小卡卡所在的城市编号以及小YY所在的城市编号。

输出格式

一共有\(M\)行，每行两个数\(Pos\)和\(Cost\)，用一个空格隔开，表示第\(i\)次聚会的地点选择在编号为\(Pos\)的城市，总共的费用是经过\(Cost\)条道路所花费的费用。

数据范围

\[N \le 500000 \\\\
M \le 500000 \\\\
\]

输入样例：

6 4
1 2
2 3
2 4
4 5
5 6
4 5 6
6 3 1
2 4 4
6 6 6

输出样例：

5 2
2 5
4 1
6 0

解题报告

题意理解

不同于一般的LCA题目,这道题目是,在一棵\(n-1\)条边的树上,有三个节点,要你求出这个三个点抵达一个汇聚点的最少代价.

---

算法解析

这道题目的核心点,就是它是由三个点构成的最短路.

为什么,它同于一般的题目,难道不是让我们直接求出三个点的最近公共祖先?

汇聚点为什么不是

\[Lca(Lca(a,b),Lca(a,c)) \\\\
或者 \\\\
Lca(Lca(a,c),Lca(b,c)) \\\\
以上选项二选一
\]

如果你真的是这么想,脑海里面只有A,B选项,那么你应该庆幸,出题人比较良心丧心病狂留下的唯一良知,他给你提出了一个样例,告诉你为什么不是这样.

因为文化课考试的时候,题目都是A,B,C或者再来一个D的单项选择题.

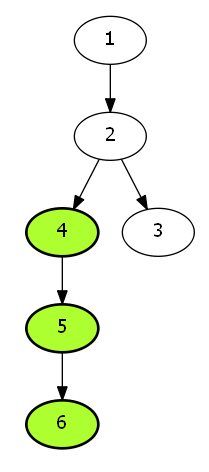
\(3\)人分别在\(4,5,6\)三个节点上面.

仔仔细细地观察一下,我们发现这道题目的汇聚点,应该是5,而不是4.

1. 假如说我们按照楼上这个错误思路,我们的三点的最近公共祖先节点,应该是4.

2. 但是最少花费,显然是在\(5\)号节点.

我们的思路居然是错误的!!!

它到底错误在了哪里.

我们要分析一下,这道题目,为什么选择的是5,而不是4?

选择\(4\),那么\(1\)号小朋友不需要行动.

选择\(5\),那么\(2,3\)号小朋友都不需要行动.

---

我们可以这么现实化这道题目.

\(2,3\)号小朋友他们是互相的知己一对狗男女,所以说,他们想要先在一起.发朋友圈,秀恩爱

所以\(2,3\)号小朋友他们会先聚集在一起

花费代价为

\[消耗距离=deep[b]+deep[c]-deep[Lca(b,c)]
\]

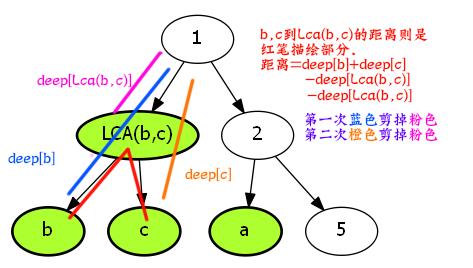
此时我们面临两大选择.

1. \(1\)号同学孤身一人走到2,3号同学相遇的地方.
2. \(2,3\)号同学一起手拉手和\(1\)号同学相遇.再秀一次恩爱,虐一下单身狗1号

假如说\(1\)号同学,与\(2,3\)号同学相隔\(L\)个距离.

我们将会发现,两大选择,会产生两大代价.

方案一

\[消耗距离=L-deep[Lca(a,Lca(b,c))]
\]

方案二

\[消耗距离=2*L-deep[Lca(a,Lca(b,c))]
\]

那么显然我们发现第一个方案是最优秀的方案.

所以说我们得出了性质,那就是.

\[ { }
消耗距离=deep[b]+deep[c]-2 \times deep[Lca(b,c)] +L-deep[Lca(a,Lca(b,c))] \\\\
其中L=deep[a]
\]

综上所述,同理其他两种方案也可以得出.

1. \(1,2\)先在一起
2. \(2,3\)先在一起
3. \(1,3\)先在一起

---

代码解析

#include <bits/stdc++.h>
using namespace std;
const int N=500000+200,M=500000*2+100;
int n,m,s,lg[N],deep[N];
struct Lca
{
	int head[M],Next[M],edge[M],tot,fa[N][22];
	void init()
	{
		memset(head,0,sizeof(head));
		tot=0;
	}
	void add_edge(int a,int b)
	{
		edge[++tot]=b;
		Next[tot]=head[a];
		head[a]=tot;
		return ;
	}
	void dfs(int x,int y)
	{
		deep[x]=deep[y]+1;
		fa[x][0]=y;
		for(int i=1; (1<<i)<=deep[x]; i++)
			fa[x][i]=fa[fa[x][i-1]][i-1];
		for(int i=head[x]; i; i=Next[i])
			if (edge[i]!=y)
				dfs(edge[i],x);
		return ;
	}
	int LCA(int x,int y)
	{
		if (deep[x]<deep[y])
			swap(x,y);
		while(deep[x]>deep[y])
			x=fa[x][lg[deep[x]-deep[y]]-1];
		if (x==y)
			return x;
		for(int k=lg[deep[x]]; k>=0; k--)
			if (fa[x][k]!=fa[y][k])
			{
				x=fa[x][k];
				y=fa[y][k];
			}
		return fa[x][0];
	}
} g1;
int main()
{
	scanf("%d%d",&n,&m);
	g1.init();
	for(int i=1; i<n; i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		g1.add_edge(a,b);
		g1.add_edge(b,a);
	}
	g1.dfs(1,0);
	for(int i=1; i<=n; i++)
		lg[i]=lg[i-1]+(1<<lg[i-1]==i);
	for(int i=1; i<=m; i++)
	{
		int x,y,z,c_x,c_y,c_z,dx,dy,dz;
		scanf("%d%d%d",&x,&y,&z);
		c_x=g1.LCA(x,y),dx=deep[x]+deep[y]-deep[c_x]+deep[z]-2*deep[g1.LCA(z,c_x)];
		c_y=g1.LCA(y,z),dy=deep[y]+deep[z]-deep[c_y]+deep[x]-2*deep[g1.LCA(x,c_y)];
		c_z=g1.LCA(x,z),dz=deep[x]+deep[z]-deep[c_z]+deep[y]-2*deep[g1.LCA(y,c_z)];
		if(dx>dy)
		    dx=dy,c_x=c_y;
		if(dx>dz)
		    dx=dz,c_x=c_z;
		printf("%d %d\n",c_x,dx);
	}
	return 0;
}