MySQL之InnoDB索引面试学习笔记

写在前面

　　想要做好后台开发，终究是绕不过索引这一关的。先问自己一个问题，InnoDB为什么选择B+树作为默认索引结构。本文主要参考MySQL索引背后的数据结构及算法原理和剖析Mysql的InnoDB索引。

索引

　　当数据量到达一定规模时，我们通常会对经常使用的字段建立索引，来加快数据的查询。首先需要强调的是索引的本质是数据结构，前辈们经过不断完善得到了几种复杂度较低并且能够降低磁盘IO的数据结构，这里要说的是B树与B+树，他们被广泛应用在文件系统与数据库系统中。

B-Tree

　 B树逻辑上是一颗多叉树，3阶B树如下：

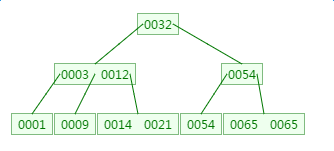
　　m阶B树满足以下几个条件：

非叶子节点最少有m/2颗子树（即B树的度为m/2）
叶子节点在同一层，每个节点最多有m-1个升序排列的key（索引列）和m个指针，key与指针相互间隔

搜索二叉树的查询复杂度为O(log2N)，而B树的复杂度为O(logm/2N)，对于N=62*1000000000个节点，如果度为1024，则log_M/2N <=4，可以说它是效率很高的数据结构。

B+树

　　B+树是B树的变种，区别有三点：

非叶子节点只存储key，不存储data；叶子节点存储所有key与data，不存储指针
叶子节点增加了顺序访问指针
每个节点最多有m个升序排列的key

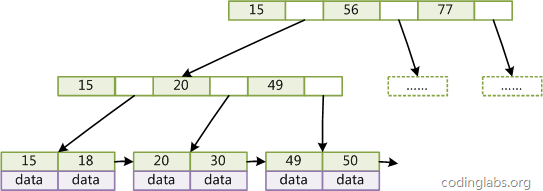
　　上述区别换来的优点包括：

非子节点可以存放更多的key，具有更好的空间局部性，提高缓存命中率
叶子节点相链便于区间查找，顺序查找替代B树的递归查找。

为什么选择B+树

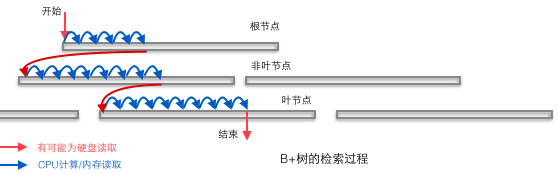
　　首先要意识到数据检索的时间主要耗费在磁盘IO（寻道时间、旋转时间）上，因此要尽量减少IO次数。对树形结构的数据来说，树的每一层代表需要一次磁盘IO查询，因此设计了“扁平”的B树与更扁的B+树。另外，由著名的局部性原理，访问的数据通常比较集中，磁盘每次IO时会预读数据，预读的长度为页（4k）的整数倍，B/B+树新建节点会申请一个页的空间，因此取一个节点只需要一次IO（非叶子节点可存储到内存中）。

索引创建过程

mysql创建索引是通过online create index，减少业务停写时间，创建索引期间业务能正常工作。

步骤：

等待当前所有事务执行结束；新事务更新数据会把新建索引记录到Row Log中
构建索引，从主表读出数据并排序。使用临时文件进行外部排序方式，单线程两路归并。
把增量数据从Row Log更新到索引表中

MySQL存储引擎

首先区分聚簇索引（按主键聚集）与非聚簇索引：

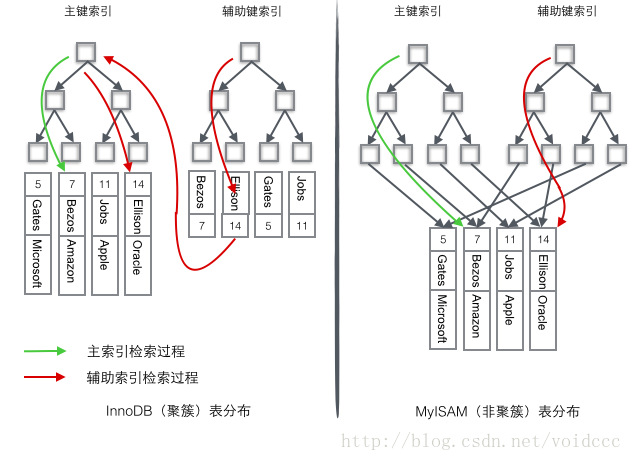
二者都使用B+树作为数据结构
聚簇索引的data存于主键索引的叶子节点中，得到key同时得到data，非聚簇索引数据存于独立的地方，叶节点保存的是数据的地址。
聚簇索引的辅助键索引（非主键索引，例如employee表中对name建索引）叶节点存储主键而非数据（为了节省空间，缺陷是需要到主键索引中二次查询）；非聚簇索引叶节点保存数据的地址。

　　聚簇索引的优势在于找到主键同时得到data，省去二次磁盘IO；另外B+树在插入或删除节点时周围节点地址会发生变化，对非聚簇索引来说需要更新所有B+树的地址指针，增加开销。

InnoDB

　　InnoDB使用聚簇索引（MyISAM使用非聚簇索引），其磁盘管理逻辑单位是Page（不同于上述内存中的页！），每个Page大小为16k，使用32位int标识，对应innoDB最大64TB的存储容量。

　　每个Page包括头部、主体、尾部三部分：

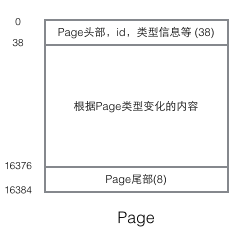
　　其中头部包括id与相邻Page指针（构成双向链表）；

　　主体即B+树节点的存储，其中包括很多Record（节点）包括四类：

主索引非叶子节点：定位Page
主索引叶子节点：包括key与该key对应的所有列（mysql表中的一行）
辅助索引非叶子节点：定位Page
辅助索引叶子节点：包括索引键值与主键值（key）

　主键选择

　　因为数据存于主索引中，要求一个节点的各条数据记录按主键顺序存放，当一页达到装载因子（15/16）会自动开辟新的页。如果使用自增主键，每次插入新纪录都顺序添加到索引节点的后续位置，否则会节点中key会一直移动。

　 最左匹配原则

　　在联合索引中对a，b两个字段建立索引（a, b），在查询时只有包括a时才会查询索引。

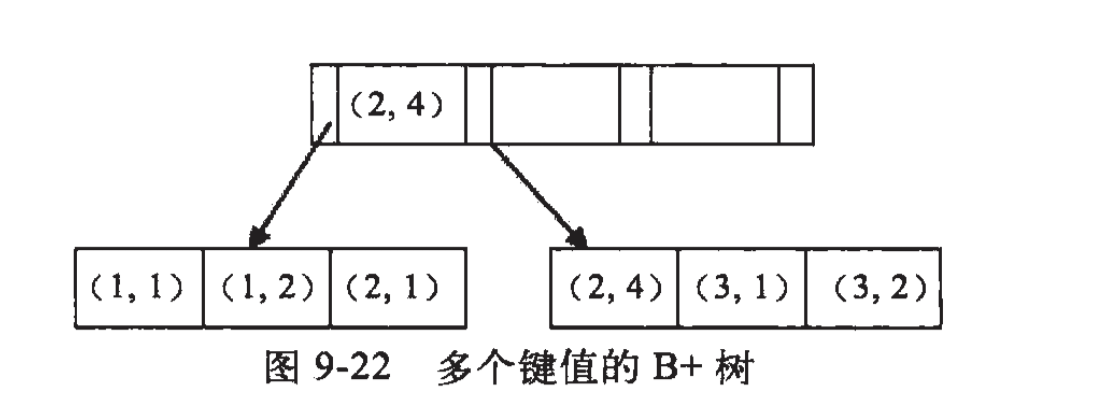
　　如上图（a, b）联合索引，在a相同时，b按顺序排列。在遇到范围查询时之后的字段会停止匹配。因为a是范围，b无序。　　