codeforces700B

CF700B Connecting Universities

题意翻译

树之王国是一个由n-1条双向路连接着n个城镇的国家，任意两个城镇间都是联通的。

在树之王国共有2k所大学坐落于不同的城镇之中。

最近，树国总统颁布了一项在大学间建立高速信息网络的法案。教育部部长以他自己的方式理解了这项法案，他发现用电缆连接各所学校是绰绰有余的。形式上来说，这项法案安排的任务的确被完成了！(贪官...)

为了能尽可能多地获取财政预算，部长打算把大学分成一对一对的，使得在各所学校间建立连接所需的电缆最长。换句话说，k对大学间的距离总和越大越好。

帮助部长完成这个任务。当然了，每所大学不能重复出现在多对里。你可以认为每条路的长度均为1。

输入格式：

输入数据的第一行包括两个整数n和k(2<=n<=200000,1<=k<=n/2)，分别表示城镇的数量以及大学数量的一半。你可以认为城镇是从1到n编号的。

第二行包括2k个整数u1，u2，...，u2k(1<=ui<=n)，表示第i所大学所在城镇编号。

接下来的n-1行中每行都包括两个整数xj，yj(1<=xj,yj<=n)，表示第j条道路连接着xj与yj两座城镇。左右的道路都是双向道路。你只能使用这些道路移动。

输出格式：

输出k对大学间最大的距离总和。

说明：

下图展示了在样例一的一种可能的结果。如果你把坐落于1号城镇的大学和坐落于6号城镇的大学连接在一起，把坐落于2号城镇的大学和坐落于5号城镇的大学连接在一起，那么距离总和为6，在样例一中是最大距离总和。

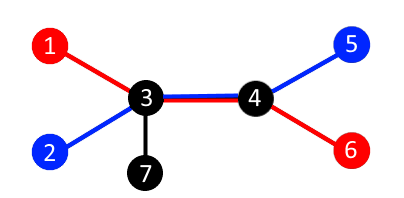
sol：对于每条边球贡献，一个点x到to的边的贡献就是to的子树中大学的数量与总数量之差的min

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
  ll s=; bool f=; char ch=' ';
  while(!isdigit(ch)) {f|=(ch=='-'); ch=getchar();}
  while(isdigit(ch)) {s=(s<<)+(s<<)+(ch^); ch=getchar();}
  return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
  if(x<) {putchar('-'); x=-x;}
  if(x<) {putchar(x+''); return;}
  write(x/); putchar((x%)+'');
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const int N=,M=;
int n,m,sz[N];
ll ans=;
int tot=,Next[M],to[M],head[N];
inline void Link(int x,int y)
{
    Next[++tot]=head[x]; to[tot]=y; head[x]=tot;
}
inline void dfs(int x,int fat)
{
    int e;
    for(e=head[x];e;e=Next[e]) if(to[e]!=fat)
    {
        dfs(to[e],x); sz[x]+=sz[to[e]]; ans+=min(sz[to[e]],m-sz[to[e]]);
    }
}
int main()
{
//    freopen("codeforces700B.in","r",stdin);
    int i,x,y;
    R(n); m=read()<<;
    for(i=;i<=m;i++) sz[read()]=;
    for(i=;i<n;i++)
    {
        R(x); R(y); Link(x,y); Link(y,x);
    }
    dfs(,);
    Wl(ans);
  return ;
}