2022-09-27：给定一个棵树， 树上每个节点都有自己的值，记录在数组nums里， 比如nums[4] = 10，表示4号点的值是10， 给定树上的每一条边，记录在二维数组edges里， 比如ed

2022-09-27：给定一个棵树，
树上每个节点都有自己的值，记录在数组nums里，
比如nums[4] = 10，表示4号点的值是10，
给定树上的每一条边，记录在二维数组edges里，
比如edges[8] = {4, 9}表示4和9之间有一条无向边，
可以保证输入一定是一棵树，只不过边是无向边，
那么我们知道，断掉任意两条边，都可以把整棵树分成3个部分。
假设是三个部分为a、b、c，
a部分的值是：a部分所有点的值异或起来，
b部分的值是：b部分所有点的值异或起来，
c部分的值是：c部分所有点的值异或起来，
请问怎么分割，能让最终的：三个部分中最大的异或值 - 三个部分中最小的异或值，最小。
返回这个最小的差值。
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]。
输出：9。

答案2022-09-27：

dfn序号。
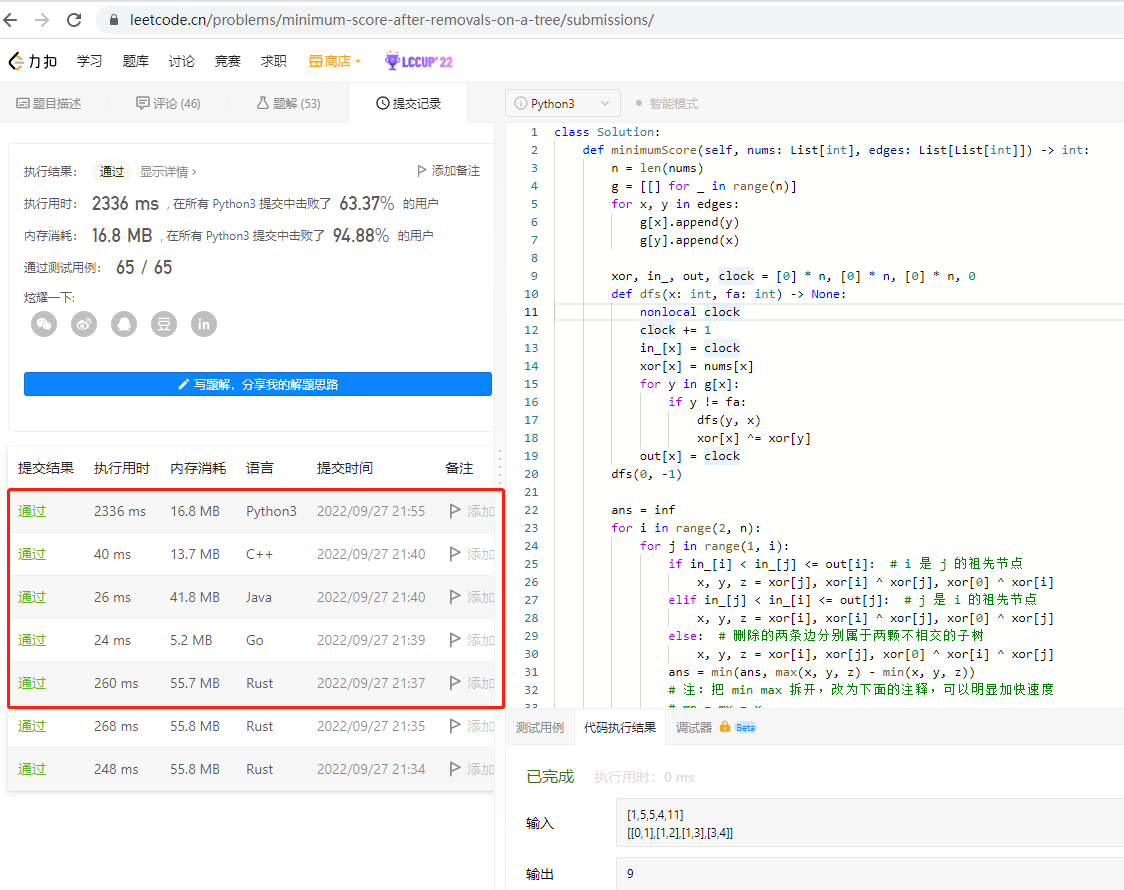
这道题来自力扣2322。力扣上测试了好几种语言的代码，go语言运行效率是最高，其次是java；rust表现不佳，原因是代码中有复制切片的行为。内存占用go是最低的，rust偏高，原因是代码中有复制切片的行为。
时间复杂度：O(n^2)。
空间复杂度：O(n)。

代码用rust编写。代码如下：

use std::iter::repeat;
fn main() {
    let mut nums = vec![1, 5, 5, 4, 11];
    let mut edges = vec![vec![0, 1], vec![1, 2], vec![1, 3], vec![3, 4]];
    let ans = minimum_score(&mut nums, &mut edges);
    println!("ans = {}", ans);
}
const MAX_VALUE: i32 = 1 << 31 - 1;
static mut cnt: i32 = 0;

fn minimum_score(nums: &mut Vec<i32>, edges: &mut Vec<Vec<i32>>) -> i32 {
    let n = nums.len() as i32;
    // 先建立图
    // ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
    let mut graph: Vec<Vec<i32>> = vec![];
    // 4个点，0、1、2、3
    // 0 : {}
    // 1 : {}
    // 2 : {}
    // 3 : {}
    for _i in 0..n {
        graph.push(vec![]);
    }
    for edge in edges.iter() {
        // a,b
        // graph.get(a).add(b);
        // graph.get(b).add(a);
        graph[edge[0] as usize].push(edge[1]);
        graph[edge[1] as usize].push(edge[0]);
    }
    // 无向边组成的无环图
    // 为了方便，就认为0是头
    // dfn[i] = ?
    let mut dfn: Vec<i32> = repeat(0).take(n as usize).collect();
    // xor[i] 以i为头的整棵树，整体异或的结果是多少？
    let mut xor: Vec<i32> = repeat(0).take(n as usize).collect();
    // size[i] 以i为头的整棵树，一共几个点？
    let mut size: Vec<i32> = repeat(0).take(n as usize).collect();

    unsafe {
        cnt = 1;
    }
    dfs(nums, &mut graph, 0, &mut dfn, &mut xor, &mut size);
    let mut ans = MAX_VALUE;
    let m = edges.len() as i32;
    let mut cut1: i32;
    let mut cut2: i32;
    let mut pre: i32;
    let mut pos: i32;
    let mut part1: i32;
    let mut part2: i32;
    let mut part3: i32;
    let mut max: i32;
    let mut min: i32;
    for i in 0..m {
        // i，要删掉的第一条边，i号边
        // edges[i][0]   edges[i][1]  dfn 谁大，谁就是删掉之后的树的头！cut1
        //      a            b                cut1
        // { a, b}
        //   0  1
        let a = edges[i as usize][0];
        let b = edges[i as usize][1];
        cut1 = if dfn[a as usize] < dfn[b as usize] {
            b
        } else {
            a
        };
        for j in (i + 1)..m {
            // j, 要删掉的第二条边，j号边
            // { c, d}
            //   0  1
            let c = edges[j as usize][0];
            let d = edges[j as usize][1];
            cut2 = if dfn[c as usize] < dfn[d as usize] {
                d
            } else {
                c
            };
            // cut1，cut2
            pre = if dfn[cut1 as usize] < dfn[cut2 as usize] {
                cut1
            } else {
                cut2
            };
            pos = if pre == cut1 { cut2 } else { cut1 };
            // 早 pre  晚 pos
            part1 = xor[pos as usize];
            // pos为头的树，是pre为头的树的子树！
            if dfn[pos as usize] < dfn[pre as usize] + size[pre as usize] {
                part2 = xor[pre as usize] ^ xor[pos as usize];
                part3 = xor[0] ^ xor[pre as usize];
            } else {
                // pos为头的树，不是pre为头的树的子树！
                part2 = xor[pre as usize];
                part3 = xor[0] ^ part1 ^ part2;
            }
            max = get_max(get_max(part1, part2), part3);
            min = get_min(get_min(part1, part2), part3);
            ans = get_min(ans, max - min);
        }
    }
    return ans;
}

fn get_max<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a > b {
        a
    } else {
        b
    }
}

fn get_min<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a < b {
        a
    } else {
        b
    }
}
// 所有节点的值，存在nums数组里
// 整个图结构，存在graph里
// 当前来到的是cur号点
// 请把cur为头，整棵树，所有节点的dfn、size、xor填好！
// 返回！
fn dfs(
    nums: &mut Vec<i32>,
    graph: &mut Vec<Vec<i32>>,
    cur: i32,
    dfn: &mut Vec<i32>,
    xor: &mut Vec<i32>,
    size: &mut Vec<i32>,
) {
    // 当前节点了！，
    dfn[cur as usize] = unsafe { cnt };
    unsafe {
        cnt += 1;
    }
    // 只是来到了cur的头部！
    xor[cur as usize] = nums[cur as usize];
    size[cur as usize] = 1;
    // 遍历所有的孩子！
    for next in graph.clone()[cur as usize].iter() {
        //有clone，会影响性能
        // 只有dfn是0的孩子，才是cur在树中的下级！！！！
        if dfn[*next as usize] == 0 {
            // cur某个孩子是next

            dfs(nums, graph, *next, dfn, xor, size);
            // next整棵树的异或和，
            xor[cur as usize] ^= xor[*next as usize];
            // next整棵树的size
            size[cur as usize] += size[*next as usize];
        }
    }
}

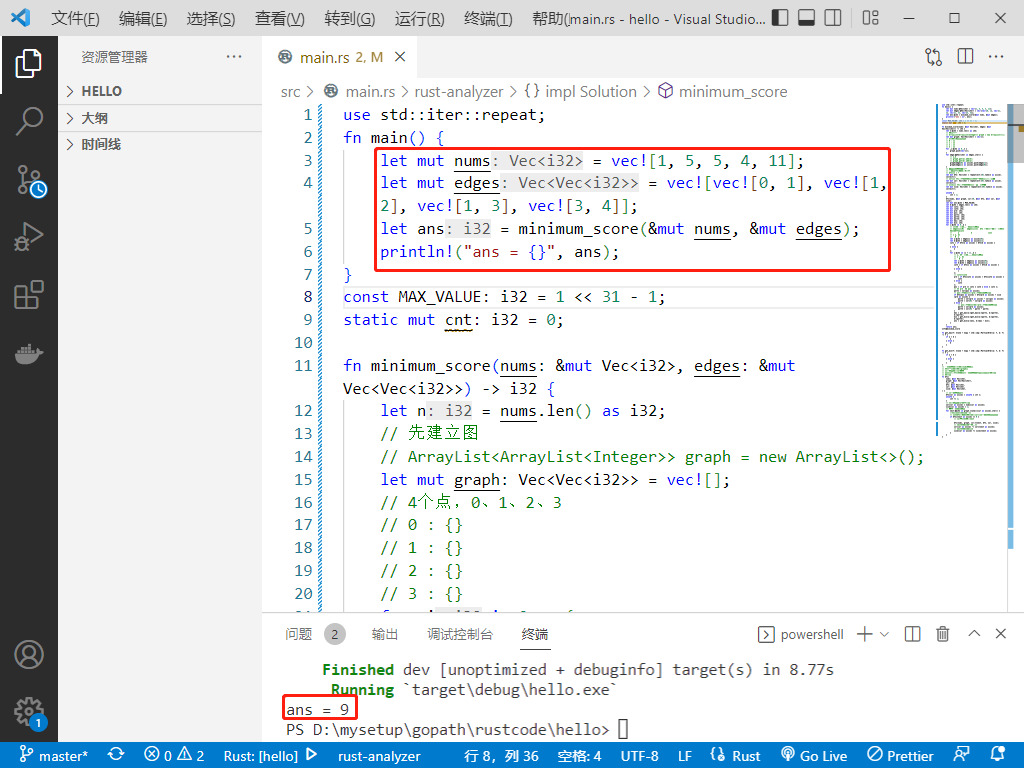
执行结果如下：

---

左神java代码