CSP-S T3函数调用

函数是各种编程语言中一项重要的概念，借助函数，我们总可以将复杂的任务分解成一个个相对简单的子任务，直到细化为十分简单的基础操作，从而使代码的组织更加严密、更加有条理。然而，过多的函数调用也会导致额外的开销，影响程序的运行效率。

某数据库应用程序提供了若干函数用以维护数据。已知这些函数的功能可分为三类：

将数据中的指定元素加上一个值；
将数据中的每一个元素乘以一个相同值；
依次执行若干次函数调用，保证不会出现递归（即不会直接或间接地调用本身）。

在使用该数据库应用时，用户可一次性输入要调用的函数序列（一个函数可能被调用多次），在依次执行完序列中的函数后，系统中的数据被加以更新。某一天，小 A 在应用该数据库程序处理数据时遇到了困难：由于频繁而低效的函数调用，系统在执行操作时进入了无响应的状态，他只好强制结束了数据库程序。为了计算出正确数据，小 A 查阅了软件的文档，了解到每个函数的具体功能信息，现在他想请你根据这些信息帮他计算出更新后的数据应该是多少。

输入格式

第一行一个正整数 n，表示数据的个数。
第二行 n个整数，第 i个整数表示下标为 i的数据的初始值为 ai。
第三行一个正整数 m，表示数据库应用程序提供的函数个数。函数从 1∼m编号。
接下来 m行中，第 j（1≤j≤m）行的第一个整数为 Tj，表示 j号函数的类型：

若 Tj=1，接下来两个整数 Pj,Vj分别表示要执行加法的元素的下标及其增加的值；
若 Tj=2，接下来一个整数 Vj 表示所有元素所乘的值；
若 Tj=3，接下来一个正整数 Cj表示 j号函数要调用的函数个数，
随后 Cj个整数 g1(j),g2(j),…,gCj(j)依次表示其所调用的函数的编号。

第 m+4 行一个正整数 Q，表示输入的函数操作序列长度。
第 m+5行 QQ 个整数 fi，第 i个整数表示第 i个执行的函数的编号。

输出格式

一行 n个用空格隔开的整数，按照下标 1∼n的顺序，分别输出在执行完输入的函数序列后，数据库中每一个元素的值。答案对 998244353 取模。

题解：

这个题，研究之后发现真的是好题；

首先题目中的调用关系提示我们应该是个有向图，同时，函数不会直接或者间接的调用自己，所以不会出现环的情况

有向图上的算法有哪些呢？拓扑排序，最后的q次调用函数，也可以写成等同于m次操作，只是他为0号，会调用q次函数，所以以0号为超级原点，建立有向图即可

题目中提示了，如果只有操作1或者只有操作2怎么办？

如果只有乘法操作，哎呀，爽歪歪，直接拓扑排序，记录最终0号节点被乘了多少次x就行了，最终序列中所有的值直接乘以x即可

如果只有加法操作呢？暂时不会

加法操作和乘法操作混在一起的时候，就比较难计算，因为加法操作会被乘法操作影响，但是，我们考虑，加法操作会被哪些乘法影响呢？他只会被自己后面进行的乘法影响，所以对于每一个加，我们是否可以计算出这个加法操作被乘法执行了多少次，执行了多少次就是加法的倍数，最后我们用被加数*倍数就可以得到加的值是多少，以下图举例：

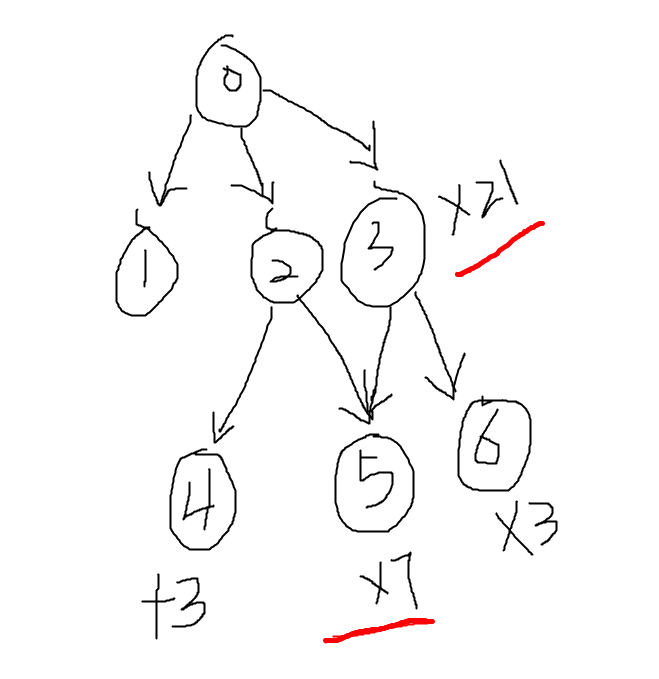
例如图中的+3操作，会被后面的*5影响，同时也会被3操作影响，当我们第一遍拓扑排序的时候，已经把每个节点的乘处理出来了，现在我们考虑怎么把+3被执行了多少次？

+3会被自己子树内的后面的乘法影响，同时还会被父亲节点后面的乘法节点影响，怎么计算呢？计cnt[v]表示v这个加法后面有多少乘法？如何递推呢？cnt[v]=cnt[v]+cnt[u]*cm，cm表示子树内目前被执行了多少次，cnt[u]表示父亲后面有多少乘法，cnt[u]*cm表示目前有多少乘法。当然，cnt[0]=1，这一点千万别忘了，如果这个值为0的话，只能计算子树内的贡献了

问题一：在做的过程中，有一个问题值得注意，既然0号节点连接其他节点，那么我们直接把0号节点放入队列中即可，为什么还需要枚举0-m呢？

因为在建图的过程中，有些节点虽然没有被0号节点调用，但是可能和最终节点连接，如果我们只把0号节点push进队列中，那么子节点有可能不能变成入度为0的点，就会有错误，换句话说，因为我们在建图的过程中，把所有点都放在图中了，但是在最终调用的时候却没有把某些点放在图中拓扑，所以会出现错误。

问题二；把没有被0号节点调用的点放入第二次拓扑中，会不会对答案产生影响呢？如下图

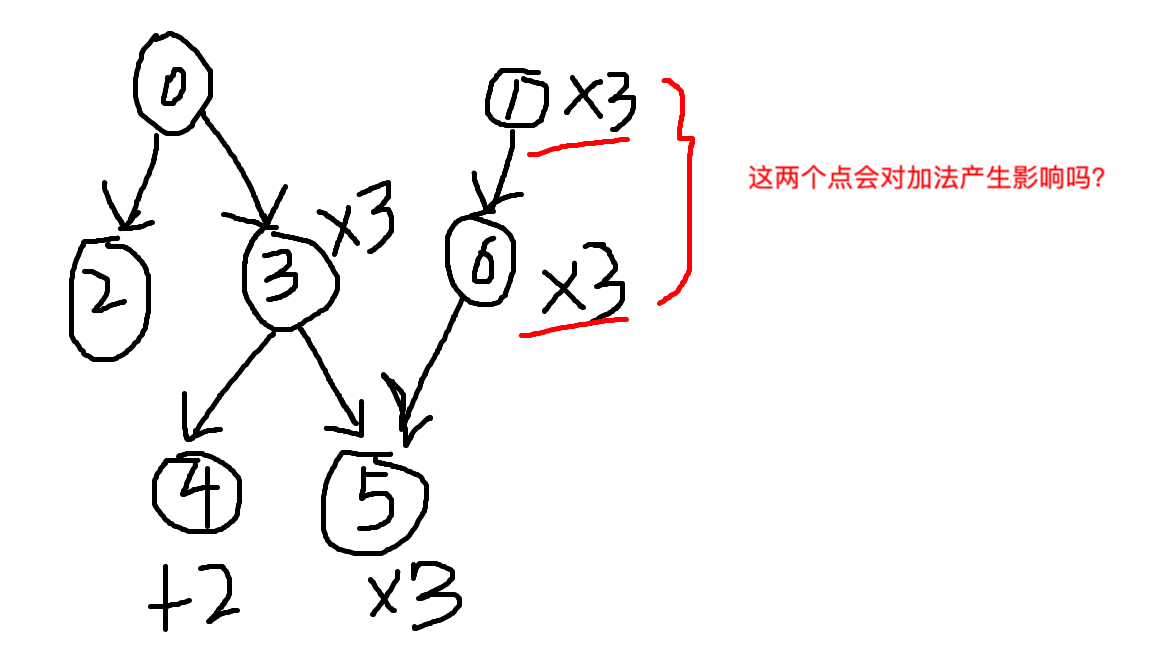
答案是不会，因为虽然乘法上会产生影响，但是我们只设定了cnt[0]=1，其他入度为0的点cnt[]的值均为0，所以根本更新不到子树