ACM - 动态规划 - UVA437 The Tower of Babylon

题解

初始时给了 \(n\) 种长方体方块，每种有无限个，对于每一个方块，我们可以选择一面作为底。然后用这些方块尽可能高地堆叠成一个塔，要求只有一个方块的底的两条边严格小于另一个方块的底的两条边，这个方块才能堆在另一个上面。

问题的思考在于每种方块有无限个，如果我们直接利用该条件问题会变得比较复杂。其实仔细考虑方块堆叠的要求，会发现这是一个约束很强的条件。

注意到，方块堆叠的要求描述的对象不只是方块本身，更细地说，它应该描述的是方块摆放方式。一个长方体方块有三个面可以作为底（另三个面为对面，面与面对应相同），选择其中一个面后又需要再分两种摆放方式。所以对每种方块应该有六种摆放方式。用向量可以描述这六种摆放方式。前两个数字表示底面的长和宽，第三个数字表示高。

\((x_i, y_i, z_i)\)
\((y_i, x_i, z_i)\)
\((y_i, z_i, x_i)\)
\((z_i, y_i, x_i)\)
\((x_i, z_i, y_i)\)
\((z_i, x_i, y_i)\)

根据方块堆叠的要求，我们可以进一步得出，每种方块摆放方式（共 \(6n\) 种）在堆叠过程中最多出现一次。否则，存在一种摆放方式至少出现了两次，对于该种方块摆放方式，无论谁在上谁在下，都会存在一个方块的底的两条边等于另一个方块的底的两条边的情况，与严格小于相悖。所以对于每种方块摆放方式，我们可以选择“摆放”或是“不摆放”。

我们进一步思考方块堆叠的要求，它要保证底的两条边都得严格小于另一底的两条边，因此我们可以先对其中一条边做一个排序，再保证“选出的所有方块”的另一条边堆叠时依次严格小于即可。也就是说可以将二维的问题通过预处理排序将为一维的问题，而且可以进一步发现该一维问题是比较典型的动态规划问题（最长上升子序列）。

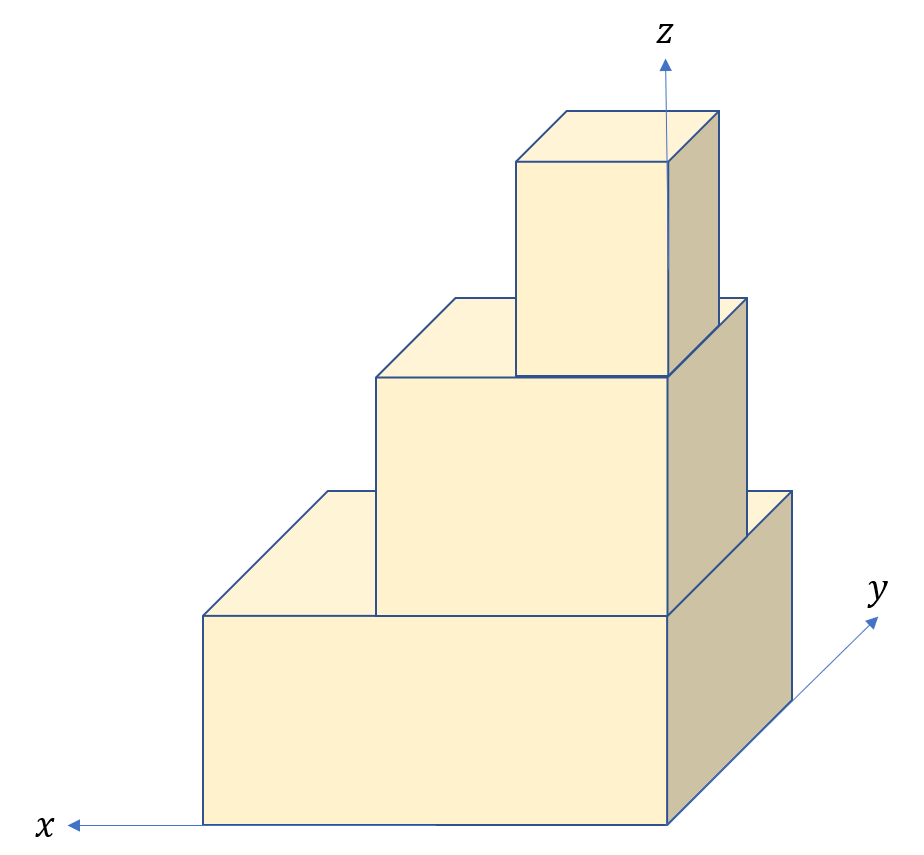
对在 \(x\) 轴上的每条边做一个排序（从大到小），然后根据 \(y\) 轴上的边的值选择“摆放”或是“不摆放”，最后要使得 \(z\) 轴上的值加和最大。使用一维 \(dp\) 数组记录状态，\(dp[i]\) 表示以第 \(i\) 个已摆放的前 \(i\) 个方块摆放方式的最大高度。

状态转移方程

\(dp[i]\) 状态表示已经“摆放”了第 \(i\) 号方块摆放方式，达到最大高度的堆叠方式可能需要垫一个方块，也可能不需要。如果垫一个方块则该方块的摆放方式只能是前面 \(i-1\) 个方块摆放方式中的一个（预处理时已将方块摆放方式排序，后面的方块一定不满足要求），由此可得状态转移方程：

\[dp[i] = \max \left( \max_{0 \leqslant j \leqslant i - 1} dp(j), 0 \right) + blocks[i].g
\]

状态搜索方向

直接将 \(dp[i]\) 从左至右依次更新即可。

程序：

#include<cstdio>

#include<cstring>

#include<algorithm>

#include<iostream>

#include<vector>

using namespace std;

int n, x, y, z, cnt = 0;

struct node {

    int c, k, g;

    node(int x, int y, int z) {

        c = x; k = y; g = z;

    }

};

vector<node> blocks;

int dp[305];

bool cmp(node a, node b) {

    if (a.c > b.c) return true;

    else if (a.c == b.c) {

        if (a.g > b.g) return true;

        else return false;

    }

    else return false;

}

int main()

{

    while (cin >> n && n != 0) {

        blocks.clear();

        for (int i = 0; i < n; ++i) {

            scanf("%d %d %d", &x, &y, &z);

            // 每个方块六种摆放方式

            blocks.push_back(node(x, y, z));

            blocks.push_back(node(y, x, z));

            blocks.push_back(node(x, z, y));

            blocks.push_back(node(z, x, y));

            blocks.push_back(node(z, y, x));

            blocks.push_back(node(y, z, x));

        }

        // 排序

        sort(blocks.begin(), blocks.end(), cmp);

        memset(dp, -1, sizeof(dp));

        int ans = -1;

        for (int i = 0; i < 6 * n; ++i) {

            dp[i] = blocks[i].g;

            for (int j = 0; j < i; ++j) {

                if (blocks[i].c < blocks[j].c && blocks[i].k < blocks[j].k)

                    dp[i] = max(dp[j] + blocks[i].g, dp[i]);

            }

            ans = max(ans, dp[i]);

        }

        printf("Case %d: maximum height = %d\n", ++cnt, ans);

    }

    return 0;

}