把语音分割为计算发音质量测度所需要的小单元时候，需要进行Viterbi对齐

Viterbi，在htk和sphinx中，也被称作token passing model

Viterbi解码图是 状态数Sm(所有状态)*时间长度(帧长度)On大小

Viterbi是对一个非常大的HMM(多个音素HMM的组合，可能是所有音素HMM的组合)进行解码

Viterbi解码，输入是On长度的帧，输出是一个状态序列，然后可以对应一个HMM

一个HMM可以代表无数个状态序列，因为其中有自环

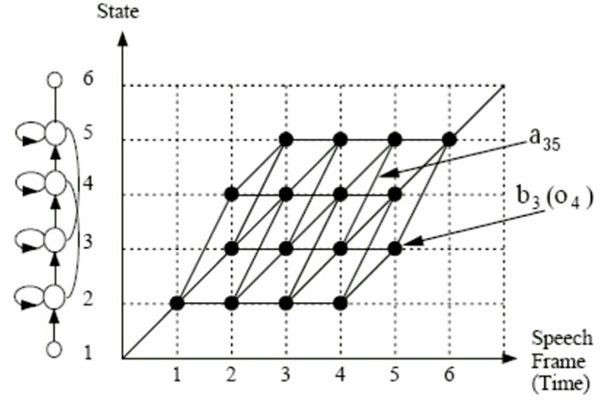
Token passing为生成hypotheses（译者注：意为可能的识别结果）的lattice（译者注：网格）提供了可能，lattice比单Best输出更有用。基于这个思想的算法称为lattice N-best。因为每个状态一个token，限制了可能得到的不同token历史记录的数量，所以他们不是最合适的。若每个模型状态对应

多个token，并且如果认为来自不同前序单词的token是不同的，就可以避免上述限制。这类算法称为word N-best 算法，经验表明它的性能可以和最优的N-best算法相当。

δi(1),πi(1)bi(ο1),假设i=5,初始状态为5且输出观察向量为ο1的概率,

ψi(1),0

δj(t),状态路径为<p1,p2,…,i,j>且概率最大时(p1,p2,…,pn未知),j的观察向量为ot的概率.假设j=9,t=15,

ψj(t),使状态路径为<p1,p2,…,i,j>概率最大的i(p1,p2,…,pn未知)

Viterbi的更多相关文章

  1. 维特比算法（Viterbi Algorithm）

      寻找最可能的隐藏状态序列(Finding most probable sequence of hidden states) 对于一个特殊的隐马尔科夫模型(HMM)及一个相应的观察序列,我们常常希望 ...

  2. 隐马尔科夫模型及Viterbi算法的应用

    作者:jostree 转载请注明出处 http://www.cnblogs.com/jostree/p/4335810.html 一个例子: 韦小宝使用骰子进行游戏,他有两种骰子一种正常的骰子,还有一 ...

  3. HMM Viterbi算法 详解

    HMM:隐式马尔可夫链   HMM的典型介绍就是这个模型是一个五元组: 观测序列(observations):实际观测到的现象序列 隐含状态(states):所有的可能的隐含状态 初始概率(start ...

  4. Viterbi algorithm

    HMM(隐马尔可夫模型)是用来描述隐含未知参数的统计模型,是一个关于时序的概率模型,它描述了一个由隐藏的马尔可夫链生成状态序列,再由状态序列生成观测序列的过程.其中,状态之间的转换以及观测序列和状态序 ...

  5. 隐马尔可夫模型（HMM）及Viterbi算法

    HMM简介   对于算法爱好者来说,隐马尔可夫模型的大名那是如雷贯耳.那么,这个模型到底长什么样?具体的原理又是什么呢?有什么具体的应用场景呢?本文将会解答这些疑惑.   本文将通过具体形象的例子来引 ...

  6. 隐马尔可夫(HMM)、前/后向算法、Viterbi算法

    HMM的模型  图1 如上图所示,白色那一行描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列,蓝紫色那一行是各个状态生成可观测的随机序列 话说,上面也是个贝叶斯网络,而贝叶斯网络中有这么一种,如下 ...

  7. HMM模型和Viterbi算法

    https://www.cnblogs.com/Denise-hzf/p/6612212.html 一.隐含马尔可夫模型(Hidden Markov Model) 1.简介 隐含马尔可夫模型并不是俄罗 ...

  8. ZH奶酪：隐马尔可夫模型学习小记——forward算法+viterbi算法+forward-backward算法（Baum-welch算法）

    网上关于HMM的学习资料.博客有很多,基本都是左边摘抄一点,右边摘抄一点,这里一个图,那里一个图,公式中有的变量说不清道不明,学起来很费劲. 经过浏览几篇博文(其实有的地方写的也比较乱),在7张4开的 ...

  9. 维特比算法（Viterbi）-实例讲解(暴力破解+代码实现)

    1.简介 维特比算法是一个通用的求序列最短路径的动态规划算法,也可以用于很多其他问题,比如:文本挖掘.分词原理.既然是动态规划算法,那么就需要找到合适的局部状态,以及局部状态的递推公式.在HMM中,维 ...

随机推荐

  1. bzoj2007 NOI2010 海拔(对偶图)

    80分(最小割)思路 先考虑如果没有题目中东南角为\(1\)那个限制的话会怎样. 那么只要让每个点的海拔都是\(0\)就行了.这样不论怎样走,最后的答案都是0. 然后再考虑那个东南角为\(1\)的限制 ...

  2. 解决MySQL5.7密码重置问题

    前言:最近活动,买了台服务器,环境什么的都弄完了,MySQL是安装的5.7的版本,连接进入的时候出现了下面的错误 这其实是MySQL5.7的一个安全机制,需要你重新设置密码. set password ...

  3. linux:awk修改输出分隔符

    file1的内容如下: a b c d e f g h 现在想要修改成 a b c:d e f g:h 则需要用到如下命令: awk -F " " '{print $1,$2,$3 ...

  4. SpringBoot文件上传

    先建工程 只勾选web和freemarker模板 最后 先看一下最终目录结构 先修改pom文件,加入common-io依赖 然后修改Application.yml文件 spring: freemark ...

  5. java 集合的总结

    集合大致可以分为两类: 一类继承Collection接口,存储的是多个孤立的元素,包括List和set: List包括ArrayList类和LinkedList类,ArrayList数组的顺序存储,而 ...

  6. 4.2、LED1、LED2交替闪烁

    #include "ioCC2530.h" //引用CC2530头文件 /***************************************************** ...

  7. Qt ------ excel 操作

    写 excel // step1:连接控件 QAxObject* excel = new QAxObject(this); excel->setControl("Excel.Appli ...

  8. Django+Uwsgi+Nginx

    一.数据库准备 yum install mariadb-server -y systemctl start mariadb   监听端口 netstat -lntup   mysql 进入 grant ...

  9. maven-compiler-plugin报错

    [INFO] Scanning for projects... [INFO] [INFO] --------------------------< cn.x:credittest >--- ...

  10. 解决gitk显示文件内容中文乱码

    解决gitk显示文件内容中文乱码 1.git config 命令 设置git gui的界面编码 git config --global gui.encoding utf-8 2.修改配置文件 在~\e ...