HDU 1384 Intervals【差分约束-SPFA】

类型：给出一些形如a−b<=k的不等式（或a−b>=k或a−b<k或a−b>k等），问是否有解【是否有负环】或求差的极值【最短/长路径】。
例子：b−a<=k1，c−b<=k2，c−a<=k3。将a，b，c转换为节点；k1，k2，k3转换为边权；减数指向被减数，形成一个有向图：

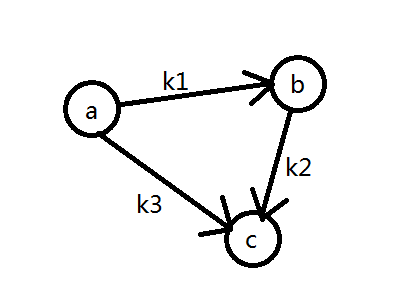
由题可得（b−a） + （c−b） <= k1+k2，c−a<=k1+k2。比较k1+k2与k3，其中较小者就是c−a的最大值。
由此我们可以得知求差的最大值，即上限被约束，此时我们拿最小的限制，也就是跑最短路；反之，求差的最小值，下限被约束，我们跑最长路。
跑最短路时：d[v]<=d[u]+w
跑最长路时：d[v]>=d[u]+w
路径中可能会存在负边，用SPFA跑。判断负环，最短最长路均可

题意：

[a,b]区间内有>=c个数，计算集合里至少多个元素

思路：

因为数据范围 0 <= ai <= bi <= 50000，可以设s[i]为i之前元素个数【不含i】,将题意转化为差分约束，s[b+1]-s[a]>=c，防止a-1出界。

求s[end]>=?，求下限，求最长路，注意数组初始化和d数组更新条件

解决不连通有两个方法：

1. 新增特殊点或在区间内以1为单位连通

2.所有点全部入队，并标记

 #include <queue>
 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 const int N=;
 int n,cnt;
 const int INF=0x3f3f3f3f;
 int head[N],d[N];
 bool vis[N];

 struct e{
     int to,next,w;
 }edge[N<<]; // 有反向边

 void add(int u,int v,int w){
     edge[cnt].w=w;edge[cnt].to=v;edge[cnt].next=head[u];head[u]=cnt++;
 }

 void init(){
     cnt=;
     memset(head,-,sizeof(head));
 }

 void SPFA(int s)
 {
     memset(d,-INF,sizeof(d));
     memset(vis,, sizeof(vis));
     queue<int> q;
     q.push(s);
     d[s]=;
     vis[s]=;
     while(q.size())
     {
         int u = q.front();q.pop();
         vis[u]=;
         for(int i=head[u];i!=-;i=edge[i].next)
         {
             int v=edge[i].to;
             int w=edge[i].w;
             if(d[v]<d[u]+w)
             {
                 d[v]=d[u]+w;
                 if(!vis[v])
                 {
                     q.push(v);
                     vis[v]=;
                 }
             }
         }
     }
 }

 int main(){
     while(scanf("%d",&n)!=EOF) {
         init();
         int st = INF, ed = -INF;
         for (int i = ; i <= n; i++) {
             int a, b, c;
             cin >> a >> b >> c;
             add(a, b + , c);
             st = min(st, a);
             ed = max(ed, b + );
         }
         for (int i = st; i < ed; i++) {
             add(i, i + , );
             add(i + , i, -);
         }
         SPFA(st);
         cout << d[ed] << endl;
     }
     return ;
 }