数据特征分析：1.基础分析概述& 分布分析

基础分析概述

几个基础分析思路：

分布分析

对比分析

统计分析

帕累托分析

正态性检测

相关性分析

分布分析

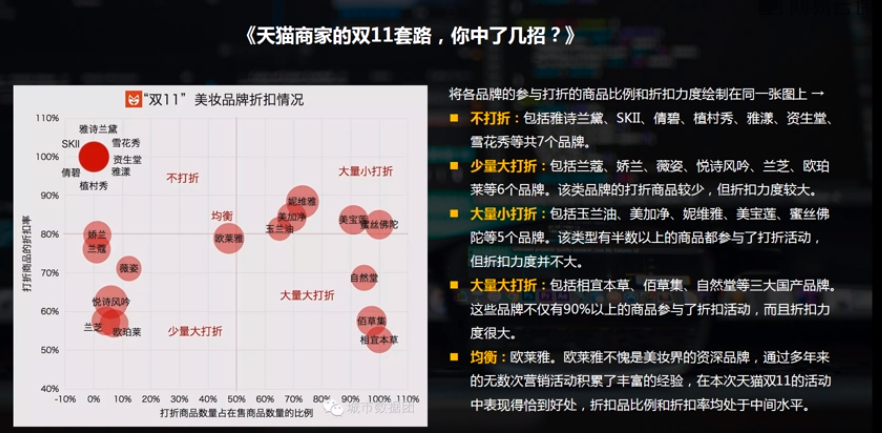
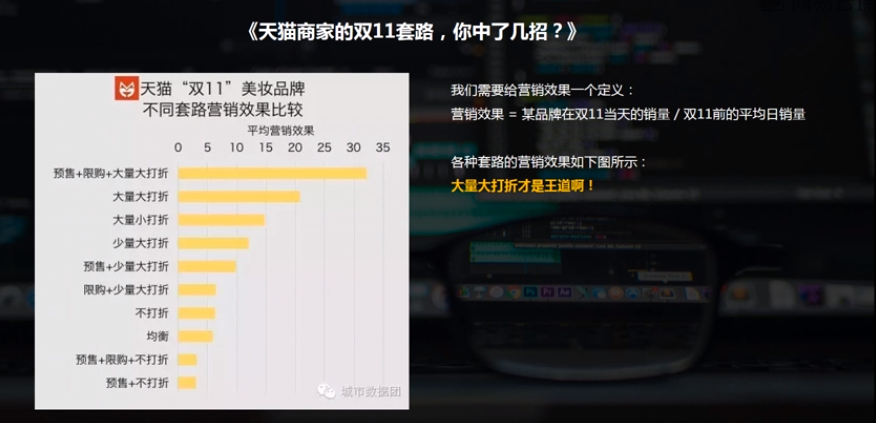
分布分析是研究数据的分布特征和分布类型，分定量数据、定性数据区分基本统计量。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline

#读取数据
data = pd.read_csv(r'C:\Users\Administrator\Desktop\python数据分析\深圳罗湖二手房信息.csv',
                   engine = 'python')
data.head()

plt.scatter（）散点图

plt.scatter(data['经度'], data['纬度'], #做个简单的三角图，按照经纬度作为它的X Y轴
                s = data['房屋单价']/500, #按照房屋的单价来控制图形的大小
                c = data['参考总价'], cmap = 'Reds',#按照参考总价来显示颜色
                alpha = 0.4)        #########plt.scatter（）散点图

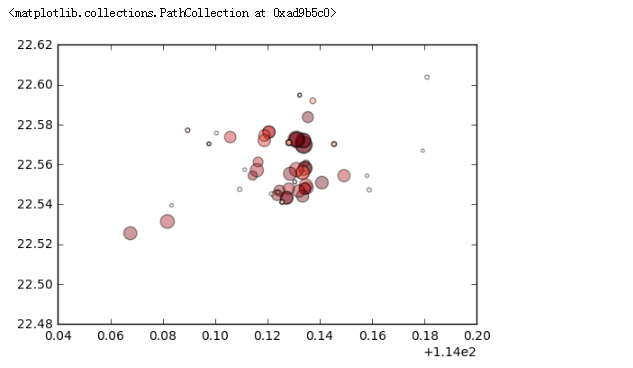
plt.scatter() 散点图

如果有底图就可以把它的位置给分布出来；点越大代表房屋的单价越高，颜色越深代表总价越高；

通过数据可见，一共8个字段
 定量字段：房屋单价，参考首付，参考总价，*经度，*纬度，*房屋编码
 定性字段：小区，朝向

1.极差

#极差
def d_range(df, *cols):
    krange = [] #空列表，为了保持它的值
    for col in cols:
        crange = df[col].max() - df[col].min()
        krange.append(crange)
    return (krange)  ##创建函数求极差
key1 = "参考总价"
key2 = "参考首付"
dr = d_range(data, key1, key2)
print("%s极差为：%f \n%s极差为：%f"% ( key1, dr[0], key2, dr[1])) #求出数据对应列的极差

参考总价极差为：175.000000
参考首付极差为：52.500000

从极差中看到销售的稳定程度

2. 频率分布情况：定量字段

（① 通过直方图直接判断分组组数）

.hist(bins = 8) 直方图

#频率分布情况（通过直方图直接判断分组组数）
data[key1].hist(bins = 8) #参考总价 简单查看数据分组，确定分组组数 --->>一般8-16组，这里按照8组为参考

可以看出主要集中在160万以上，60万以下。

频率分布的划分方式：直方图可以快速的看到它的排列情况，把它拆分：分组划分

（②求出分组区间）

 pd.cut(data[key1], 10, right = False).value_count(sort=True) sort=True <-等价-> ascending=True

#频率分布情况，分组区间 ；对参考总价进行分组。
gcut = pd.cut(data[key1], 10, right = False) #分成10份，是否包含末端值选False
gcut  #type(gcut)-->>Series
gcut_count = gcut.value_counts(sort = False) #做一个统计，不排序
gcut_count

# pd.cut(x, bins, right)：按照组数对x分组，且返回一个和x同样长度的分组dataframe，right → 是否右边包含，默认True
# 通过groupby查看不同组的数据频率分布

data['%s分组区间'% key1] = gcut.values
data.head()

（③ 求出目标字段下频率分布的其他统计量  --->>>  频数，频率，累计频率）

分组情况，做累计频率的分组情况

r_zj = pd.DataFrame(gcut_count)
r_zj

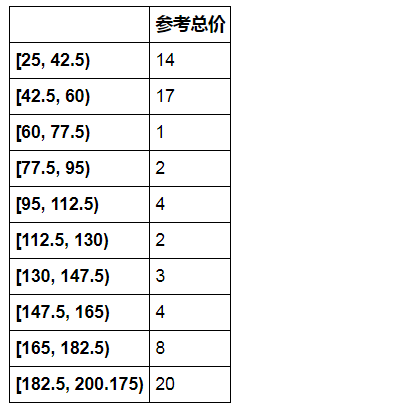
.apply(lambda x:"%.2f%%"% (x*100)) 以百分比显示

.style.bar(subset = ['频率', '累计频率']) 在格子中的条形图

#区间出现频率
r_zj = pd.DataFrame(gcut_count)
r_zj.rename(columns = {gcut_count.name:'频数'}, inplace = True) #重命名下，修改频数字段名
r_zj['频率'] = r_zj['频数']/r_zj['频数'].sum()       #计算频率
r_zj['累计频率'] = r_zj['频率'].cumsum()     #计算累计频率
r_zj['频率%'] = r_zj['频率'].apply(lambda x:"%.2f%%"% (x*100)) #以百分比显示频率
r_zj['累计频率%'] = r_zj['累计频率'].apply(lambda x:"%.2f%%"% (x*100)) #以百分比显示累计频率
r_zj.style.bar(subset = ['频率', '累计频率']) #可视化显示

（④ 绘制频率直方图）

r_zj['频率'].plot(kind = 'bar',figsize = (12, 2),grid = True,color = 'k',alpha = 0.4 ) 直方图

for i, j, k in zip(range(x), y, m):     plt.text(i - 0.1, j + 0.01, '%i'% k, color = 'k')

#直方图
r_zj['频率'].plot(kind = 'bar',
                figsize = (12, 2),
                grid = True,
                color = 'k',
                alpha = 0.4 ) #plt.title('参考总价分布频率直方图')
x = len(r_zj)
y = r_zj['频率']
m = r_zj['频数']

for i, j, k in zip(range(x), y, m):
    plt.text(i - 0.1, j + 0.01, '%i'% k, color = 'k')  #-0.1 、+0.01是调整它的位置的
#添加频率标签

频率分布情况 - 定性字段

（ ① 通过计数统计判断不同类别的频率）

# 频率分布情况 - 定性字段 -->> ① 通过计数统计判断不同类别的频率
cx_g = data['朝向'].value_counts(sort = True)
print(cx_g)
# 可视化显示
r_cx = pd.DataFrame(cx_g)
r_cx.rename(columns ={cx_g.name:'频数'}, inplace = True)  # 修改频数字段名
r_cx['频率'] = r_cx / r_cx['频数'].sum()  # 计算频率
r_cx['累计频率'] = r_cx['频率'].cumsum()  # 计算累计频率
r_cx['频率%'] = r_cx['频率'].apply(lambda x: "%.2f%%" % (x*100))  # 以百分比显示频率
r_cx['累计频率%'] = r_cx['累计频率'].apply(lambda x: "%.2f%%" % (x*100))  # 以百分比显示累计频率
r_cx.style.bar(subset=['频率','累计频率'], color='#d65f5f',width=100)

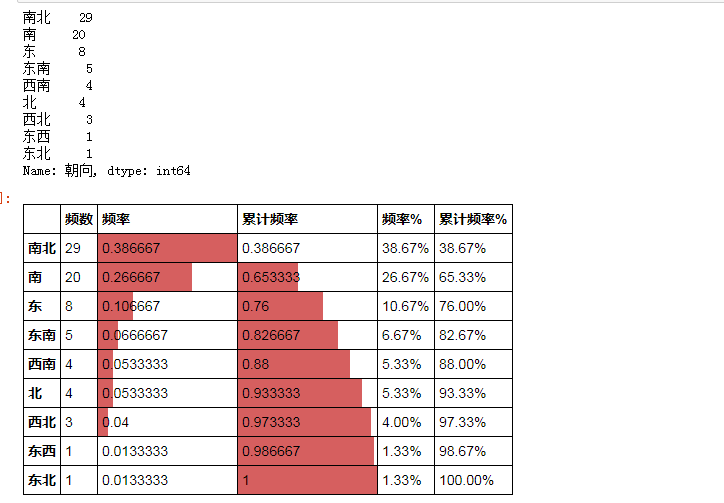
（ ② 绘制频率直方图、饼图）

.plot 由Series、DataFrame直接绘制图表；   plt.pie() 绘制饼图

# 频率分布情况 - 定量字段
# ② 绘制频率直方图、饼图

plt.figure(num = 1,figsize = (12,2))
r_cx['频率'].plot(kind = 'bar',
                 width = 0.8,
                 rot = 0,
                 color = 'k',
                 grid = True,
                 alpha = 0.5)
plt.title('参考总价分布频率直方图')
# 绘制直方图

plt.figure(num = 2)
plt.pie(r_cx['频数'],
       labels = r_cx.index,
       autopct='%.2f%%',
       shadow = True)
plt.axis('equal') #调整它的形状
# 绘制饼图