【Java】 大话数据结构(10) 查找算法(1)（顺序、二分、插值、斐波那契查找）

本文根据《大话数据结构》一书，实现了Java版的顺序查找、折半查找、插值查找、斐波那契查找。

注：为与书一致，记录均从下标为1开始。

顺序表查找

顺序查找

 顺序查找(Sequential Search)：从第一个到最后一个记录依次与给定值比较，若相等则查找成功。

　　顺序查找优化：设置哨兵，可以避免每次循环都判断是否越界。在数据量很多时能提高效率。

　　时间复杂度：O(n)，n为记录的数。

以下为顺序查找算法及其优化的Java代码：

package Sequential_Search;
/**
 * 顺序表查找
 * 数组下标为0的位置不用来储存实际内容
 * @author Yongh
 *
 */
public class Sequential_Search {
	/*
	 * 顺序查找
	 */
	public int seqSearch(int[] arr,int key) {
		int n=arr.length;
		for(int i=1;i<n;i++) {  //i从1开始
			if(key==arr[i])
				return i;
		}
		return 0;
	}
	/*
	 * 顺序查找优化，带哨兵
	 */
	public int seqSearch2(int[] arr,int key) {
		int i=arr.length-1;
		arr[0]=key;  //将arr[0]设为哨兵
		while(arr[i]!=key)
			i--;
		return i;  //返回0说明查找失败
	}

	public static void main(String[] args) {
		int[] arr = {0,45,68,32,15};
		Sequential_Search aSearch = new Sequential_Search();
		System.out.println(aSearch.seqSearch(arr, 15));
		System.out.println(aSearch.seqSearch(arr, 45));
	}
}

　

Sequential_Search

有序表查找

折半查找（二分查找）

折半查找，又称作二分查找。必须满足两个前提：

1.存储结构必须是顺序存储 
2.关键码必须有序排列

假设数据按升序排列。从中间项与关键值（key）开始对比，若关键值（key）>中间值，则在右半区间继续查找，反之则左半区间继续查找。以此类推，直至找到匹配值，或者查找内无记录，查找失败。

时间复杂度：O(logn)，可从二叉树的性质4推得。

折半查找的Java实现代码：

package OrderedTable_Search;
/**
 * 折半查找
 * @author Yongh
 *
 */
public class BinarySearch {
	public int binarySearch(int[] arr,int n,int key) {
		int low=1;
		int high=n;
		while(low<=high) {
			int mid = (low+high)/2;
			if(arr[mid]<key)
				low=mid+1;   //要+1
			else if(arr[mid]>key)
				high=mid-1;  //要-1
			else
				return mid;
		}
		return 0;
	}

	public static void main(String[] args) {
		int[] arr = {0,1,16,24,35,47,59,62,73,88,99};
		int n=arr.length-1;
		int key=62;
		BinarySearch aSearch = new BinarySearch();
		System.out.println(aSearch.binarySearch(arr, n, key));
	}
}

　　

BinarySearch

插值查找

对于表长较大，关键字分布比较均匀的查找表来说，可以采用插值查找：

　　将折半查找中代码的第12行

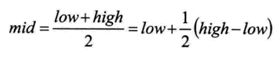
　　改进为：

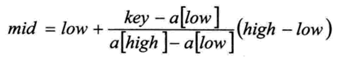
　　改进后的第12行代码如下：

int mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low]);/*插值*/

　　注意：关键字分布不均匀的情况下，该方法不一定比折半查找要好。

斐波那契查找

　　斐波那契数列如下所示：

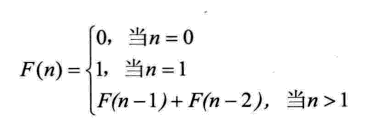
　　斐波那契查找原理与前两种相似，仅仅改变了中间结点（mid）的位置，mid不再是中间或插值得到，而是位于黄金分割点附近，即mid=low+F(k-1)-1（F代表斐波那契数列），如下图所示：

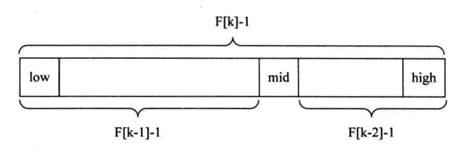
　　对F(k-1)-1的理解：

　　由斐波那契数列 F[k]=F[k-1]+F[k-2] 的性质，可以得到 （F[k]-1）=（F[k-1]-1）+（F[k-2]-1）+1 。该式说明：只要顺序表的长度为F[k]-1，则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段，即如上图所示。从而中间位置为mid=low+F(k-1)-1

　　类似的，每一子段也可以用相同的方式分割，从而方便编程。

　　但顺序表长度n不一定刚好等于F[k]-1，所以需要将原来的顺序表长度n增加至F[k]-1。这里的k值只要能使得F[k]-1恰好大于或等于n即可，由以下代码得到：

while(n>fib(k)-1)
	k++;

　　顺序表长度增加后，新增的位置（从n+1到F[k]-1位置），都赋为n位置的值即可。

　　时间复杂度：O(logn)

以下为具体的Java代码，还有不理解的地方可看对应处的注释：

package OrderedTable_Search;
/**
 * 斐波那契查找
 * 下标为0位置不存储记录
 * 顺便编写了斐波那契数列的代码
 * @author Yongh
 *
 */
public class FibonacciSearch {
	/*
	 * 斐波那契数列
	 * 采用递归
	 */
	public static int fib(int n) {
		if(n==0)
			return 0;
		if(n==1)
			return 1;
		return fib(n-1)+fib(n-2);
	}

	/*
	 * 斐波那契数列
	 * 不采用递归
	 */
	public static int fib2(int n) {
		int a=0;
		int b=1;
		if(n==0)
			return a;
		if(n==1)
			return b;
		int c=0;
		for(int i=2;i<=n;i++) {
			c=a+b;
			a=b;
			b=c;
		}
		return c;
	}

	/*
	 * 斐波那契查找
	 */
	public static int fibSearch(int[] arr,int n,int key) {
		int low=1;	//记录从1开始
		int high=n;     //high不用等于fib(k)-1，效果相同
		int mid;

		int k=0;
		while(n>fib(k)-1)	//获取k值
			k++;
		int[] temp = new int[fib(k)];	//因为无法直接对原数组arr[]增加长度，所以定义一个新的数组
		System.arraycopy(arr, 0, temp, 0, arr.length); //采用System.arraycopy()进行数组间的赋值
		for(int i=n+1;i<=fib(k)-1;i++)    //对数组中新增的位置进行赋值
			temp[i]=temp[n];  

		while(low<=high) {
			mid=low+fib(k-1)-1;
			if(temp[mid]>key) {
				high=mid-1;
				k=k-1;  //对应上图中的左段，长度F[k-1]-1
			}else if(temp[mid]<key) {
				low=mid+1;
				k=k-2;  //对应上图中的右端，长度F[k-2]-1
			}else {
				if(mid<=n)
					return mid;
				else
					return n;		//当mid位于新增的数组中时，返回n
			}
		}
		return 0;
	}
	public static void main(String[] args) {
		int[] arr = {0,1,16,24,35,47,59,62,73,88,99};
		int n=10;
		int key=59;
		System.out.println(fibSearch(arr, n, key));  //输出结果为：6
	}
}