用Excel建模进行决策树分析
决策树(Decision Tree)在机器学习中也是比较常见的一种算法,最早的决策树算法是ID3,改善后得到了C4.5算法,进一步改进后形成了我们现在使用的C5.0算法,综合性能大幅提高。
算法核心:为每一次分裂确定一个分裂属性。ID3采用的是“信息增益”为度量来选择分裂属性的。
本文在Excel中建模进行决策树分析,属于基础的决策树学习,有兴趣的可以在SPSS Modeler和Python中进行操作。
树模型(又称决策树或者树结构模型):基本思想和方差分析中的变异分解极为相似。
目的(基本原则):将总研究样本通过某些牲(自变量取值)分成数个相对同质的子样本。每一子样本因变量的取值高度一致,相应的变异/杂质尽量落在不同子样本间。所有树模型的算法都遵循这一基本原则。
不同树模型差异:差异在于对变异/杂质的定义不同。比如P值、方差、熵、Gini指数(基尼指数)、Deviance等作为测量指标。
决策树图例
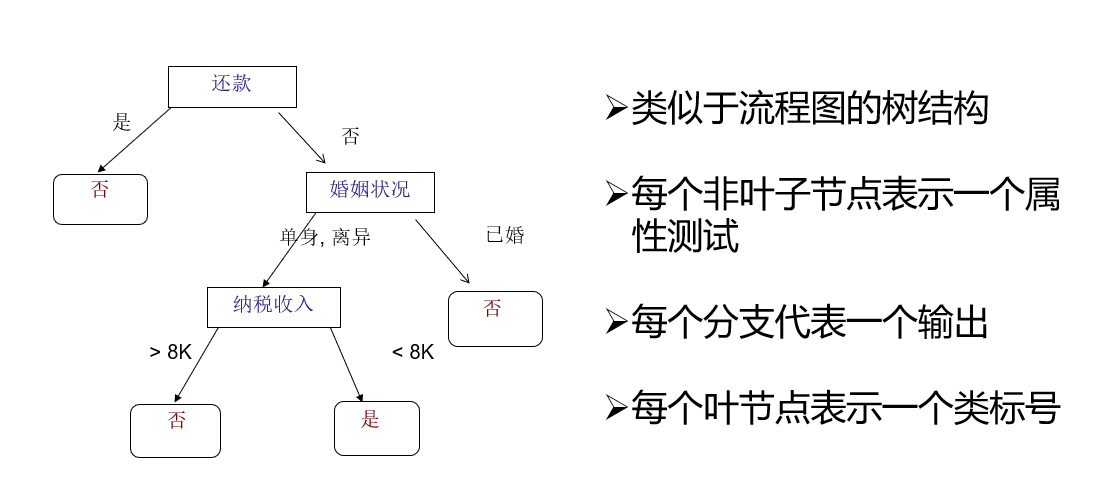
现在我们来分析天气、温度、湿度、风这些属性对打球的影响
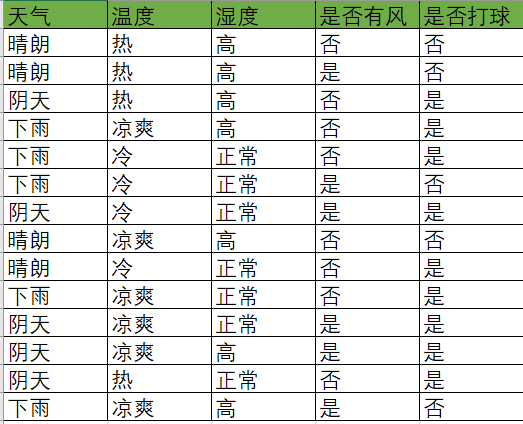
首先确定样本集信息熵,然后计算各个属性的信息增益进行对比分析。
熵:数据集中的不确定性、突发性或随机性的程度的度量。当一个数据集中的记录全部都属于同一类的时候,则没有不确定性,此时熵为0。
信息增益:按照某个属性A把数据集S分裂,所得到的信息增益等于数据集S的熵减去各个子集的熵的加权和。
计算是否打球的概率:
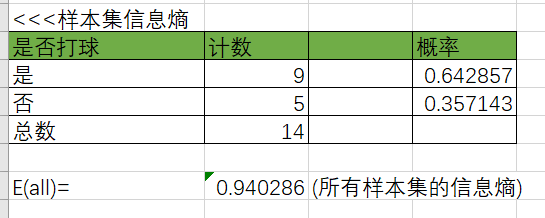
计算天气对打球的影响:


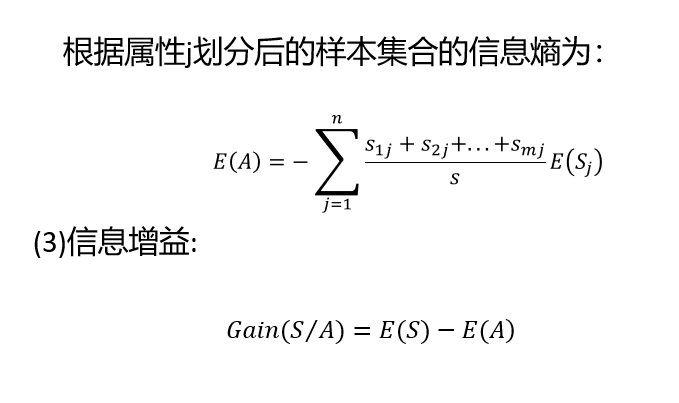
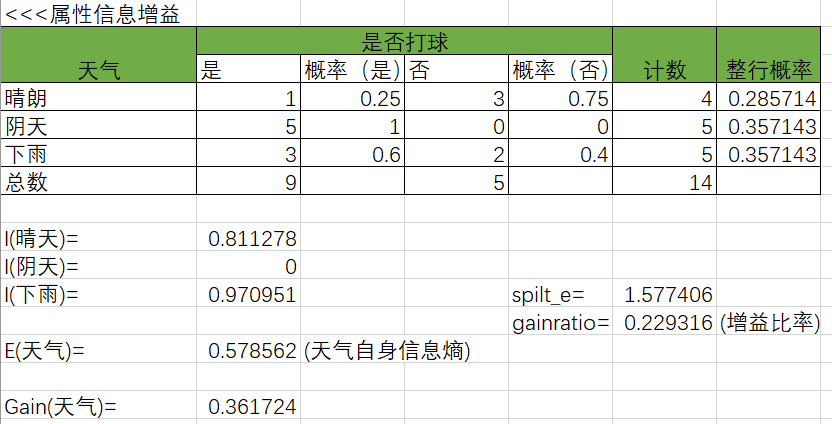
I(晴天)=-0.25*log(0.25,2)-0.75*log(0.75,2)=0.811278
E(天气)=0.285714*0.811278+0.357143*0+0.357143*0.70951=0.578562
Gain(天气)=E(all)-E(天气)=0.940286-0.578562=0.361724
经计算得出天气的信息增益为0.361724,温度、湿度和风计算步骤类似
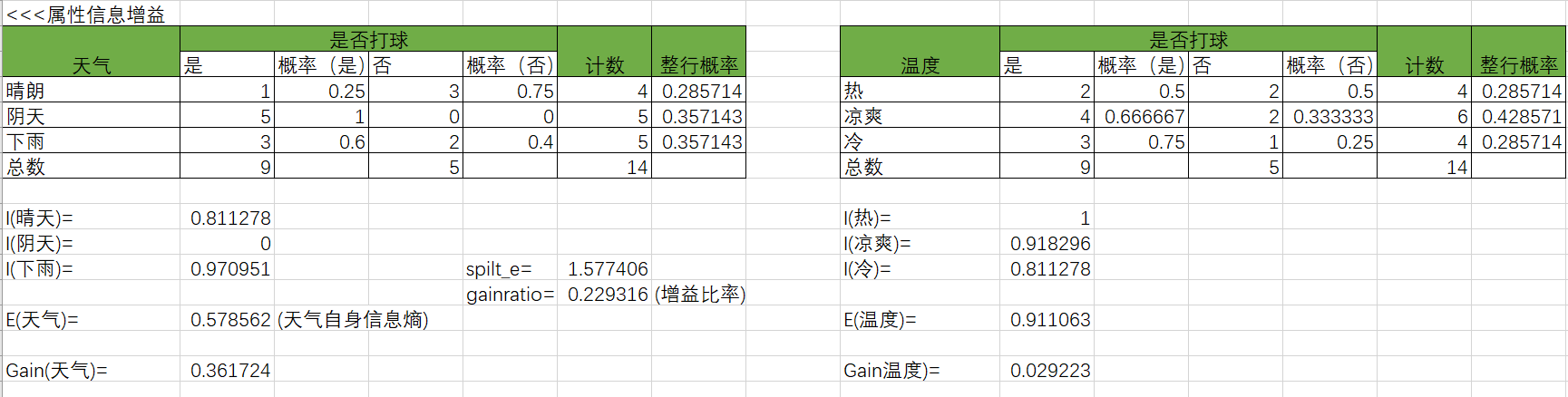

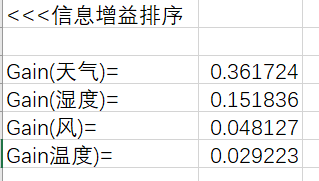
对各属性的信息增益进行降序排序,选择最大的作为分裂属性
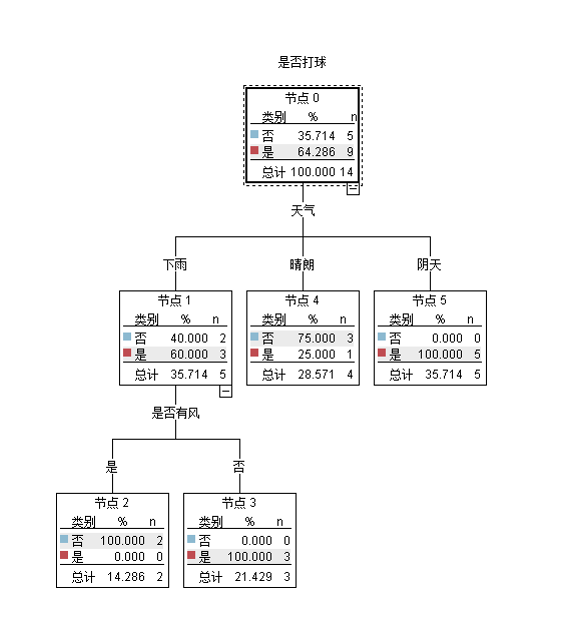
用Excel建模进行决策树分析的更多相关文章
- (转载)微软数据挖掘算法:Microsoft 决策树分析算法(1)
微软数据挖掘算法:Microsoft 目录篇 介绍: Microsoft 决策树算法是分类和回归算法,用于对离散和连续属性进行预测性建模. 对于离散属性,该算法根据数据集中输入列之间的关系进行预测. ...
- 决策树分析、EMV(期望货币值)
名称:决策树分析.EMV(期望货币值) 定义:它利用了概率论的原理,并且利用一种树形图作为分析工具.其基本原理是用决策点代表决策问题,用方案分枝代表可供选择的方案,用概率分枝代表方案可能出现的各种结果 ...
- (原创)大数据时代:基于微软案例数据库数据挖掘知识点总结(Microsoft 决策树分析算法)
随着大数据时代的到来,数据挖掘的重要性就变得显而易见,几种作为最低层的简单的数据挖掘算法,现在利用微软数据案例库做一个简要总结. 应用场景介绍 其实数据挖掘应用的场景无处不在,很多的环境都会应用到数据 ...
- 从Excel读取数据,然后分析相似的数据,多线程处理(多线程比较相似的字符串,统计出相似的数量及字符串)
之前的jar包有问题,现已修改. 需要的jar包,已修改 自己去Maven中央仓库下载jar包. excel数据: 直接上代码. 程序再度优化了一遍.之后如果想再度精准,可能需要建模,最近没空继续做了 ...
- ShellExecuteEX打开iqy文件导致excel hang的原因分析
1. 问题 当在console中调用API ShellExecuteEx打开"test.iqy"文件时,发现excel会hang住,console退出后excel才会响应,但直接双 ...
- CVE-2011-0104 Microsoft Office Excel缓冲区溢出漏洞 分析
漏洞简述 Microsoft Excel是Microsoft Office组件之一,是流行的电子表格处理软件. Microsoft Excel中存在缓冲区溢出漏洞,远程攻击者可利用此 ...
- java 导入Excel -- 套路及代码分析
一.思路分析 1.我们要做导入,实际上也就是先文件上传,然后读取文件的数据. 2.我们要有一个导入的模板,因为我们导入的Excel列要和我们的数据字段匹配上,所以我们要给它来一个规定,也就是模板. 3 ...
- CVE-2011-0104:Microsoft Office Excel 栈溢出漏洞修复分析
0x01 前言 上一篇讲到了 CVE-2011-0104 漏洞的成因和分析的方法,并没有对修复后的程序做分析.之后在一次偶然的情况下,想看一看是怎么修复的,结果却发现了一些问题 环境:修复后的 EXC ...
- EXCEL应用之商机分析:企业商机分析模板免费用
一.分析背景 商机是订单的来源,因此抓住每个销售机会,就可以更多地赢得交易.商机管理可以说是业务环节中最为关键的一步.每个企业都有自己的商机阶段划分,从销售人员接触客户.发现商机.跟进商机.推进销售 ...
随机推荐
- DOM 讲解
DOM,全称documention,文档意思 ,就是把整个html文档当成一个对象来操作,里面有很多方法,如getElementByid(),getElementByid().innerText(); ...
- 手机与PC的影音相互播放(DLNA/UPNP)
DLNA:全称是DIGITAL LIVING NETWORK ALLIANCE(数字生活网络联盟), 旨在解决个人PC,消费电器,移动设备在内的无线网络和有线网络的互联互通,使得数字媒体和内容服务的无 ...
- 好消息:手机上也可以使用Firebug功能了
做前端开发的小伙伴儿应该对火狐浏览器提供的Firebug工具很熟悉了吧,但是你知道怎么在手机上使用Firebug的控制台功能么(^_-) 现在谷歌浏览器提供了可以在电脑上模拟移动端界面的功能,但是在开 ...
- MySQL中int(M)和tinyint(M)数值类型中M值的意义
在一开始接触MySQL数据库时,对于int(M)及tinyint(M)两者数值类型后面的M值理解是最多能够插入数据库中的值不能大于M: 后来工作后,也是一边学习一边使用,之后的理解是其中的M的意思是插 ...
- 关于在项目中使用spring data redis与jedis的选择
项目中需要用到redis,主要用来作为缓存,redis的客户端有两种实现方式,一是可以直接调用jedis来实现,二是可以使用spring data redis,通过spring的封装来调用. 应该使用 ...
- 【剑指offer】二进制中1的个数
输入一个整数,输出该数二进制表示中1的个数.其中负数用补码表示. 思路:将原数字与1按位进行与操作. public class Solution { public int NumberOf1(int ...
- Consul之:服务健康监测
服务注册 - 服务进程在注册中心注册自己的位置.它通常注册自己的主机和端口号,有时还有身份验证信息,协议,版本号,以及运行环境的详细资料. 服务发现 - 客户端应用进程向注册中心发起查询,来获取服务的 ...
- java 字节码 指令集 汇编(转)
https://blog.csdn.net/github_35983163/article/details/52945845 网上找的没有指令码这列 自己把它加上 更方便查阅 指令从0x00-0xc ...
- Zabbix 卸载包 采用yum方式
- ueditor 正在读取目录及网络链接错误
环境 ueditor1_3_5-gbk-net .NET版本3.5 如果把项目直接改成4.0不会出现这样的问题,查看 问题1:正在读取目录 找到ueditor/ueditor.config.js 找 ...
