HDU 5663 Hillan and the girl (莫比乌斯反演 + 分块)

题意：给定n，m，求，其中F(x)=0,，如果x是完全平方数，否则是1。

析：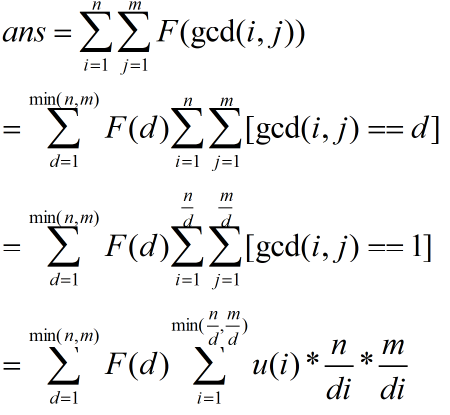

由于按照题意的F，不好筛选，所以我们反过来，F(x)，x是平方数，就是1，否则是0。

这个是可以预处理出来的，可以用筛选。

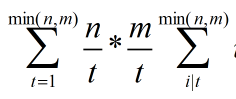这一部分，可以分块来做，所以时间复杂度就降下来了。

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
//#define all 1,n,1
#define FOR(i,x,n)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 1e7 + 5;
const int maxm = 2e4 + 10;
const LL mod = 100000007;
const int dr[] = {-1, 1, 0, 0, 1, 1, -1, -1};
const int dc[] = {0, 0, 1, -1, 1, -1, 1, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}

bool vis[maxn];
int prime[maxn], mu[maxn];
int sum[maxn];

void Moblus(){
  mu[1] = 1;  int tot = 0;
  for(int i = 2; i < maxn; ++i){
    if(!vis[i])  prime[tot++] = i, mu[i] = -1;
    for(i  nt j = 0; j < tot; ++j){
      int t = i * prime[j];
      if(t >= maxn)  break;
      vis[t] = 1;
      if(i % prime[j] == 0)  break;
      mu[t] = -mu[i];
    }
  }
  int t = sqrt(maxn + 0.5);
  for(int i = 1; i <= t; ++i){
    int x = i * i;
    for(int j = x, k = 1; j < maxn; j += x, ++k)
      sum[j] += mu[k];
  }
  for(int i = 1; i < maxn; ++i)  sum[i] += sum[i-1];
}

int main(){
  Moblus();
  int T;  scanf("%d", &T);
  while(T--){
    scanf("%d %d", &n, &m);
    if(n > m)  swap(n, m);
    LL ans = (LL)n * m;
    for(int i = 1, det; i <= n; i = det + 1){
      det = min(n/(n/i), m/(m/i));
      ans -= (LL)(sum[det]-sum[i-1]) * (m/i) * (n/i);
    }
    printf("%I64d\n", ans);
  }
  return 0;
}