非线性规划的Matlab 解法

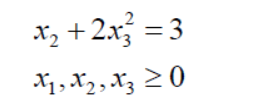
编写M 文件fun1.m 定义目标函数

function f=fun1(x);
%   定义目标函数
f=sum(x.^)+;
%   .^2是矩阵中的每个元素都求平方。^2是求矩阵的平方或两个相同的矩阵相乘，要求矩阵为方阵。

编写M文件fun2.m定义非线性约束条件

function[g,h]=fun2(x);
%定义非线性约束条件
g=[-x()^+x()-x()^
    x()+x()^+x()^-];
%非线性约束不等式条件
h=[-x()-x()^+
    x()+*x()^-];

编写主程序文件example2.m 如下：

[x,y]=fmincon('fun1',rand(,),[],[],[],[],zeros(,),[],'fun2',optimset('largescale','off'))
%这是对寻优函数搜索方式的设定，
%LargeScale指大规模搜索，off表示在规模搜索模式关闭，Simplex指单纯形算法，on表示该算法打开。
%display指结果方式，有四种off | iter | notify | final，
%iter大概是指中间结果每步都显示，一般选择final显示最终结果。在MATLAB运行窗口直接输入optimset可显示所有可设置的参数及对应的可选择的参数值。