线性可分支持向量机--SVM （1）

给定线性可分的数据集

假设输入空间(特征向量)为，输出空间为。
输入
表示实例的特征向量，对应于输入空间的点；
输出
表示示例的类别。

线性可分支持向量机的定义：

通过间隔最大化或者等价的求出相应的凸二次规划问题得到的分离超平面

以及决策函数：

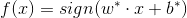
*什么是间隔最大化呢？
首先需要定义间隔，下面介绍了函数间隔和几何间隔，几何间隔可以理解为训练点到超平面的距离，二维中就是点到直线的距离，我们要做的就是最小化几何间隔。

函数间隔和几何间隔

函数间隔
给定训练数据集T和超平面（w， b）
定义超平面（w，b）关于点（xi， yi）的函数间隔：

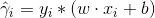
*函数间隔的理解：
描述了点x距离超平面的远近，对于正确分类的点来说，这个式子与函数间隔是相等的。因此，函数间隔可以表示分类预测的正确性和确信度。
但是，由于函数间隔会随着w， b 的改变而改变。例如，（w，b）和（2w， 2b）刻画的是同一个超平面，但是函数间隔却变为之前的2倍。因此要引入几何间隔的概念。

定义超平面（w，b）关于训练数据集T的函数间隔：

几何间隔
当样本点（xi, yi)被正确分类时，点xi与超平面（w，b）的距离可以表示为：

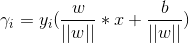
（可以联系二维空间中点到直线的距离来理解）
所以定义超平面（w，b）关于点（xi， yi）的几何间隔：

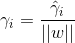
定义超平面（w，b）关于训练数据集T的几何间隔:

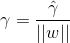
如图：

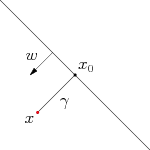
*几何间隔的理解：
几何间隔其实就是对函数间隔的规范化，联系计算点到直线的公式，几何间隔计算出来的就是欧几里得距离。

间隔最大化

间隔最大化可以写束最优化问题：

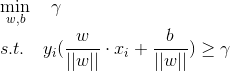
因为我们想要每一个最大化超平面（w，b）关于训练数据集的集合间隔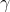
约束条件表示的是超平面（w， b）距离每个训练样本点的距离都至少是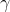
代入函数间隔和几何间隔的关系，得到：

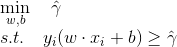
不妨取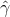= 1，那么问题就变成了最大化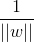了，而

为什么取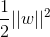呢？下面化简的时候就知道了。
那么我们得到凸二次规划问题如下：

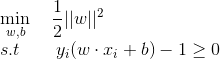
*取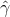 = 1的原因和影响：
原因就是上面说到的函数间隔会随着 w 的改变而改变，所以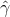的取值其实是不会影响最终的结果的，只需要优化 w 就可以了。
影响是，如果取函数间隔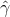 = 1，那么满足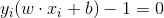的点就是支持向量（最上面图中虚线上的两个点）

学习的对偶算法

将上面的二次规划问题转换成对偶问题（参考拉格朗日对偶性(Lagrange duality)），首先引入拉格朗日函数

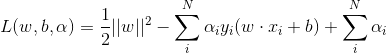
原始问题是极小极大问题：

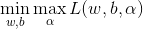
对偶问题是极大极小问题：

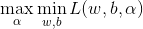
原理：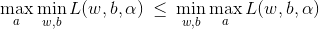
通过求对偶问题的最大值即可求得元问题的最小值

对偶问题的求解：

（1）求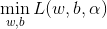
对w，b求导得到：

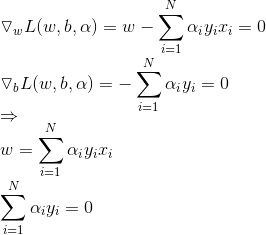
得到Lagrange函数：

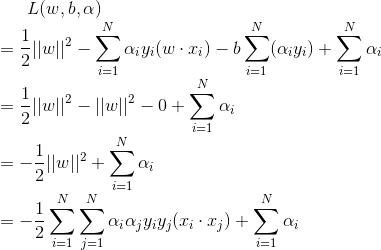
即：

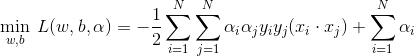
(2)求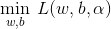的极大，即是对偶问题：

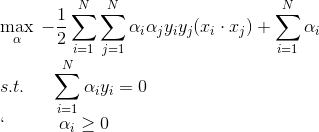
即对偶问题为：

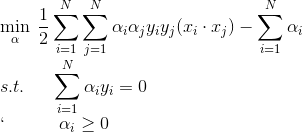
解出w， b

设求出了最优的一组解
其中至少有一个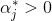,可以求出最优的w, b
理由（反证法）(参考拉格朗日乘子（Lagrange multify）和KKT条件)：
假如，则由可知，w = 0,这肯定不是最优解
因此， 至少有一个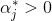，求得最优的w， b：

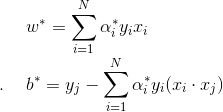
分类决策函数可以写成：

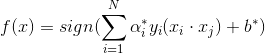
算法的综述：