数学--数论--HDU 5382 GCD？LCM？（详细推导，不懂打我）

Describtion

First we define:

(1) lcm(a,b), the least common multiple of two integers a and b, is the smallest positive integer that is divisible by both a and b. for example, lcm(2,3)=6 and lcm(4,6)=12.

(2) gcd(a,b), the greatest common divisor of two integers a and b, is the largest positive integer that divides both a and b without a remainder, gcd(2,3)=1 and gcd(4,6)=2.

(3) [exp], exp is a logical expression, if the result of exp is true, then [exp]=1, else [exp]=0. for example, [1+2≥3]=1 and [1+2≥4]=0.

Now Stilwell wants to calculate such a problem:

F(n)=∑i=1n∑j=1n [ lcm(i,j)+gcd(i,j)≥n ]S(n)=∑i=1nF(i)

Find S(n) mod 258280327.

Input

The first line of the input contains a single number T, the number of test cases.

Next T lines, each line contains a positive integer n.

T≤105, n≤106.

Output

T lines, find S(n) mod 258280327.

Sample Input

8

1

2

3

4

10

100

233

11037

Sample Output

1

5

13

26

289

296582

3928449

213582482

推导详细

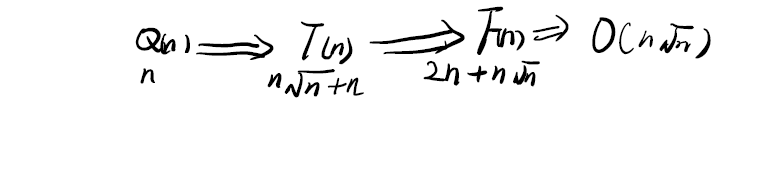
强烈建议：不赞成网上像我前面的因素和求Q(N)，这里的先求因子个数再用快速幂求解，但是这里的不同因子个数恰好可以用线性筛求解，但是在其余题目中不一定恰好可以使用，应该使用积性函数的性质直接使用线性筛，这样时间复杂度上少了一个快速幂。

好久没用scanf， printf 超时，然后写上了，忘了换行，题解叫上过来，我的就一直wa，写了对拍也是对的，我都懵了，感叹造化弄人的时候，一点一点用标程替换，知道吧printf换掉我就明白了，我太难了，凌晨1.30了，还满怀兴奋。睡不着。

#include <bits/stdc++.h>
using namespace std;

const int mxn = 1010010;
bool vis[mxn];
long long pri[100000], G[mxn], tot;
long long low[mxn];
long long T[mxn], F[mxn], S[mxn];
//线性筛求解G[]
void shai()
{
    tot = 1;
    memset(vis, 0, sizeof(vis));
    low[1] = 1;
    G[1] = 1;
    for (int i = 2; i <= mxn; i++)
    {
        if (!vis[i])
        {
            pri[tot++] = i;
            low[i] = i;
            G[i] = 2;
        }

        for (int j = 1; j <= tot && pri[j] * i <= mxn; j++)
        {
            vis[i * pri[j]] = 1;
            if (i % pri[j] == 0) //不互质
            {
                low[i * pri[j]] = low[i] * pri[j];
                if (i == low[i]) //p^K次幂，由递推求解
                    G[i * pri[j]] = 2;
					//p^k只能拆成 1 *p^k 和p^k * 1其余的情况不GCD不等于1
                else
                    G[i * pri[j]] = G[i / low[i]] * G[pri[j] * low[i]];
                break;
            }
            low[i * pri[j]] = pri[j];
            G[i * pri[j]] = G[i] * G[pri[j]];
        }
    }
}
void go()
{
    //因数枚举求解T，这里的枚举是一个很好用的技巧
    memset(T, 0, sizeof(T));
    for (int i = 1; i <= mxn; i++)
    {
        for (int j = i; j <= mxn; j += i)
        {
            T[j] = (T[j] + G[j / i - 1]) % 258280327;
        }
    }
    //递推求F，S
    S[1] = F[1] = 1;
    for (int i = 2; i <= mxn; i++)
    {
        F[i] = (((F[i - 1] + 2 * i - 1) % 258280327 - T[i - 1]) % 258280327 +258280327) % 258280327;
        S[i] = (S[i - 1] + F[i]) % 258280327;
        //cout << i << " " << S[i] << endl;
    }
}

int main()
{
    shai();
    go();
    int t;
    cin >> t;
    while (t--)
    {
        int k;
        scanf("%d", &k);
        printf("%lld\n", S[k]);
    }
    return 0;
}