机器学习、深度学习中的信息熵、相对熵（KL散度）、交叉熵、条件熵

信息熵

　　信息量和信息熵的概念最早是出现在通信理论中的，其概念最早是由信息论鼻祖香农在其经典著作《A Mathematical Theory of Communication》中提出的。如今，这些概念不仅仅是通信领域中的基础概念，也被广泛的应用到了其他的领域中，比如机器学习。

　　信息量用来度量一个信息的多少。和人们主观认识的信息的多少有些不同，这里信息的多少用信息的在一个语境中出现的概率来定义，并且和获取者对它的了解程度相关，概率越大认为它的信息量越小，概率越小认为它的信息量越大。用以下式子定义：

$I(x) = -\log p(x)$

　　信息熵用来描述一个信源的不确定度，也是信源的信息量期望。它实际上是对这个信源信号进行编码的理论上的平均最小比特数（底数为2时）。

　　式子定义如下（log 的底数可以取2、e等不同的值，只要底数相同，一般是用于相对而言的比较）：

$H(X) = E_{x\sim X}[I(x)]$

$= E_{x\sim X}[-\log x]$

$\displaystyle = -\sum\limits_{x_i\in X}[p(x_i)\log p(x_i)]$

　　《Deep Learning》的解释是：它给出了对依据概率分布P生成的符号进行编码所需的比特数在平均意义上的下界。

　　我的理解：信息（符号）出现概率越高，编码理应给它少一些比特数，和有较低的信息量相符合（由上面的信息量式子算出）。信息出现概率越低，编码时可以把它的优先级放后一些，也就是给它分配更长一些的码，和有较高的信息量相符合。反应了人们对信息的编码长度和信息的信息量是成正相关的，因为它符合这样一个事实：概率低→定义信息量高，概率低→定义编码长度长。所以信息的信息量就可以在一定程度上度量信息需要编码的长度，信源分布的信息量期望（信息熵）也就度量了一个信源平均需要的编码长度。

　　当然能发出信号的信源只是信息的一个语境而已。信息熵可以在很多语境下定义，只要有信息。

　　比如：一篇文章的字母的信息熵，那语境$X$就是在这篇文章下的所有字母，$x_i$就是每个字母，$p(x_i)$就是每个字母在文章中出现的频率。

　　又比如：小王在盒子里放了一个红球。小明知道盒子里的球色可能是红、黑、蓝三者之一，小红知道盒子里的球色是红、黑二者之一。那小明在这个游戏中所知道的信息的信息熵的语境$X$就是这三种可能性，得$H(X)  = 1.584$（以2为底）。同理，小红是二种可能性，得$H(X)  = 1.0$。如果这时候小王告诉他们：盒子里放的不是黑球。对于小明来说，可能性变成了二种，$H(X)  = 1.0$，和之前相比信息熵减少了，获得的信息量就是$1.584 - 1.0 = 0.584$。而对于小红，$H(X)$变为了0，获得信息量就是1.0。

　　这里又要问了，比如对小明来说，之前“盒子的球是黑色的”这个论断用信息量算出来$I(x) = -\log (1/3) = 1.584$呀，为什么小王告诉的消息“盒子里不是黑球”使小明获得的信息量不是这个数值？而是0.584？我懒得研究了，以后有时间再说吧。

　　另外，接近确定的分布有较低的熵；接近均匀分布的概率分布有较高的熵。如图：

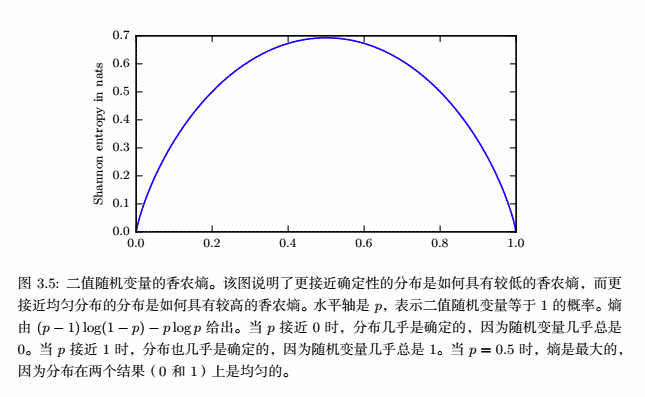
　　因此可以推出，在信源中出现的消息的种数一定时，这些消息出现的概率全都相等时，有信源的信息熵最大。则可以推出信息熵的范围：

$\displaystyle 0\le H(X) \le -\sum\limits^{n}\frac{1}{n}\log(\frac{1}{n}) = \log(n)$，$n$是不同信息数

相对熵（KL散度）

　　相对熵原本在信息论中度量两个信源的信号信息量的分布差异。

　　而在机器学习中直接把其中的信息量等概念忽略了，当做损失函数，用于比较真实和预测分布之间的差异。其实用别的式子来比较分布之间的差异也行，因为损失函数的目的只是为了减小模型预测分布和真实分布的差异而已。只要符合分布差异越大，函数值越大的式子应该都行。

定义

　　式子定义如下（这里用期望的形式定义，底数用e）：

　　$\displaystyle D_{KL}(P||Q) = E_{x\sim P}[\log \frac{P(x)}{Q(x)}] = E_{x\sim P}[\log P(x) - \log Q(x)]$

　　《Deep Learning》中的解释是：在离散型变量的情况下，KL散度衡量的是，当我们用一种被设计成能够使得概率分布Q产生的消息的长度最小的编码，发送包含由概率分布P产生的符号的消息时，所需要的额外信息量。

　　我的理解：

　　1、用使得P分布产生的消息长度最小的编码，来发送P分布产生的消息时。因为对于某个符号$x$，它的编码的信息量是$-\log P(x)$，它的概率是$P(x)$，所以P分布平均每个符号要编码的信息量就是$\sum\limits_{x\in P}[-P(x)\log P(x)] = H(P)$，就是P分布的信息熵。

　　2、用使得Q分布产生的消息长度最小的编码，来发送P分布产生的消息时。因为对于某个符号$x$，它的编码的信息量是$-\log Q(x)$，它的概率是$P(x)$，所以P分布平均每个符号要编码的信息量就是$\sum\limits_{x\in P}[-P(x)\log Q(x)] = H(P, Q)$，实际上是P和Q的交叉熵（后面提到）。

　　3、那么额外信息量就是2和1之差了，所以有：

　　$\displaystyle D_{KL}(P||Q) = \sum\limits_{x\in P}[-P(x)\log Q(x)] - \sum\limits_{x\in P}[-P(x)\log P(x)]$

$= E_{x\sim P}[\log P(x) - \log Q(x)] $

$\displaystyle = E_{x\sim P}[\log \frac{P(x)}{Q(x)}] $

　　显然当两个分布相同时，它们的KL散度为0.

非对称

　　KL散度不是一个对称量，即对于某些$P$和$Q$：$D_{KL}(P||Q) \not= D_{KL}(Q||P)$。所以使用它们来做损失函数，最小化后的效果是不一样的。

　　如下是《Deep Learning》中，使用$D_{KL}(P||Q)$ 和 $D_{KL}(Q||P)$最小化后拟合真实分布的比较图：

　　直观理解上图：

　　1、对于$D_{KL}(p||q)$，因为优化的分布是$q$而：

$\displaystyle D_{KL}(p||q) = \sum\limits_{x\in p}[-p(x)\log q(x)] - \sum\limits_{x\in p}[-p(x)\log p(x)]$

　　其中后一项不变化，所以$q$需要尽可能地靠近$p$，就产生了一个平均，得到左图。

　　2、对于$D_{KL}(q||p)$，因为优化的分布是$q$而：

$\displaystyle D_{KL}(q||p) = \sum\limits_{x\in q}[-q(x)\log p(x)] - \sum\limits_{x\in q}[-q(x)\log q(x)]$

　　其中后一项会变化，所以$q$不但需要尽可能地靠近$p$，而且$q$分布的交叉熵也要尽可能地小，就使得$q$分布更加不平均（概率尽可能集中到一点），得到右图。

非负

　　由Jenson不等式可证明KL散度非负，首先引出Jenson不等式：

　　令非负函数$f(x)$，有：

$\displaystyle\int_{-\infty}^{\infty}f(x) dx = 1$

　　如果$g(x)$是任意可测函数，并且$\varphi(x)$为下凸函数，那么有Jenson不等式如下：

$\displaystyle\varphi(\int_{-\infty}^{\infty}g(x)f(x)dx) \leq \int_{-\infty}^{\infty}\varphi(g(x))f(x)dx$

　　转换成期望的形式就是：

$\displaystyle\varphi(E_{x\sim f(x)}g(x)) \leq E_{x\sim f(x)}\varphi(g(x))$

　　在KL散度中，由于$-\log (x)$是严格下凸函数，且$\int p(x)dx = 1, \int q(x)dx = 1$，所以有：

$\displaystyle D_{KL}(p||q) = - \int p(x)\log \frac{q(x)}{p(x)}dx$

$\displaystyle \leq -ln\int p(x)\frac{q(x)}{p(x)}dx$

$\displaystyle = -ln\int q(x)dx = - ln1 = 0$

交叉熵

　　如上面提到过，交叉熵式子定义：

$H(P, Q) = -E_{x\sim P(x)}\log Q(x)$

　　由上面可知，假如$P$是真实分布，当使用$D_{KL}(P||Q)$作为损失函数时，因为只含$P$的那一项并不会随着拟合分布$Q$的改变而改变。所以这时候损失函数可以使用$H(P, Q)$来代替简化。

　　另外，由于$H(P, Q) = D_{KL}(P||Q) + H(P)$，可看出$H(P, Q)$非负且比H(P)大。

条件熵

　　为了便于表达，和前面的交叉熵、相对熵等不太一样，条件熵$H(Y|X)$中的$X$和$Y$并不是分布，而是随机变量。$H(Y|X)$表示在已知随机变量 $X$的条件下随机变量 $Y$的不确定性。注意，这里的$X$并不是某个确定值，而是随机变量，所以在计算熵的时候要对所有$H(Y|X=x)$进行求和。所以条件熵定义如下：

$H(Y|X)=\displaystyle\sum\limits_{x}P(X=x)H(Y|X=x)$

$\displaystyle=\sum\limits_{x} P(X=x)\sum\limits_{y}P(Y=y|X=x)\log \frac{1}{P(Y=y|X=x)}$
$\displaystyle=-\sum\limits_{x} \sum\limits_{y}P(X=x)P(Y=y|X=x)\log P(Y=y|X=x)$
$\displaystyle=- \sum\limits_{x,y}P(Y=y,X=x)\log P(Y=y|X=x)$

　　实际上定义的就是在所有$X$的条件下，$Y$的混乱度的平均值。

参考资料

　　1. 信息量和信息熵的理解

　　2. 详解机器学习中的熵、条件熵、相对熵和交叉熵

　　3. 《Deep Learning》