FPGA开平方的实现

3种方法：

1.JPL近似的实现方法

`timescale 1ns / 1ps
module    complex_abs#(parameter N=)(
      clk,
      syn_rst,
      dataa,
      datab,
      ampout);

input    clk;
input    [N-:]    dataa;
input    [N-:]    datab;
input    syn_rst;
output    reg    [N-:]ampout;

reg [N-:]dataa_reg ;
reg [N-:]datab_reg ;
wire [N-:]dataa_abs ;
wire [N-:]datab_abs ;
reg [N-:]dataabs_max,dataabs_min ;
reg [N-:]absmin_3 ;

 always @(posedge clk)
   begin
       if(syn_rst == 'b1)
           begin
               dataa_reg <= 'd0 ;
               datab_reg <= 'd0 ;
           end
       else
         begin
             dataa_reg <= dataa ;
               datab_reg <= datab ;
           end
   end

 assign dataa_abs = (dataa_reg[] == 'b1) ? (31'd0-dataa_reg[N-:]) : dataa_reg[N-:] ;
 assign datab_abs = (datab_reg[] == 'b1) ? (31'd0-datab_reg[N-:]) : datab_reg[N-:] ;  

 always @(posedge clk)
   begin
        if(dataa_abs > datab_abs)
             begin
                  dataabs_max <= dataa_abs ;
                  dataabs_min <= datab_abs ;
                  absmin_3 <= {'b0,datab_abs}+{datab_abs,1'b0} ;
             end
        else
          begin
                  dataabs_max <= datab_abs ;
                  dataabs_min <= dataa_abs ;
                  absmin_3 <= {'b0,dataa_abs}+{dataa_abs,1'b0} ;
             end
   end

 always @(posedge clk)
   begin
        if(absmin_3 > {'b0,dataabs_max})
             ampout <= {'b0,dataabs_max} - {4'b0,dataabs_max[N-:]} + {'b0,dataabs_min[N-2:1]} ;
        else
          ampout <= {'b0,dataabs_max} + {4'b0,dataabs_min[N-:]} ;
   end             

endmodule

2.调用IP模块的cordic算法实现效果

可选模式可以是fraction或者intergalactic

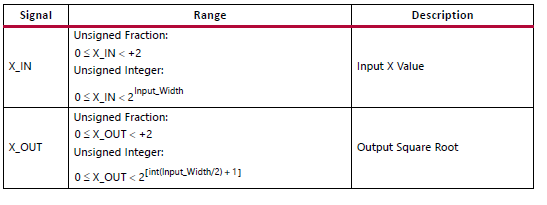
工程中输入数据的范围是远大于2的，于是我们可以采用实现方法是将所有的数据先归一化成-2~2之间，然后再进一步的采用cordic模块

IP的配置如下

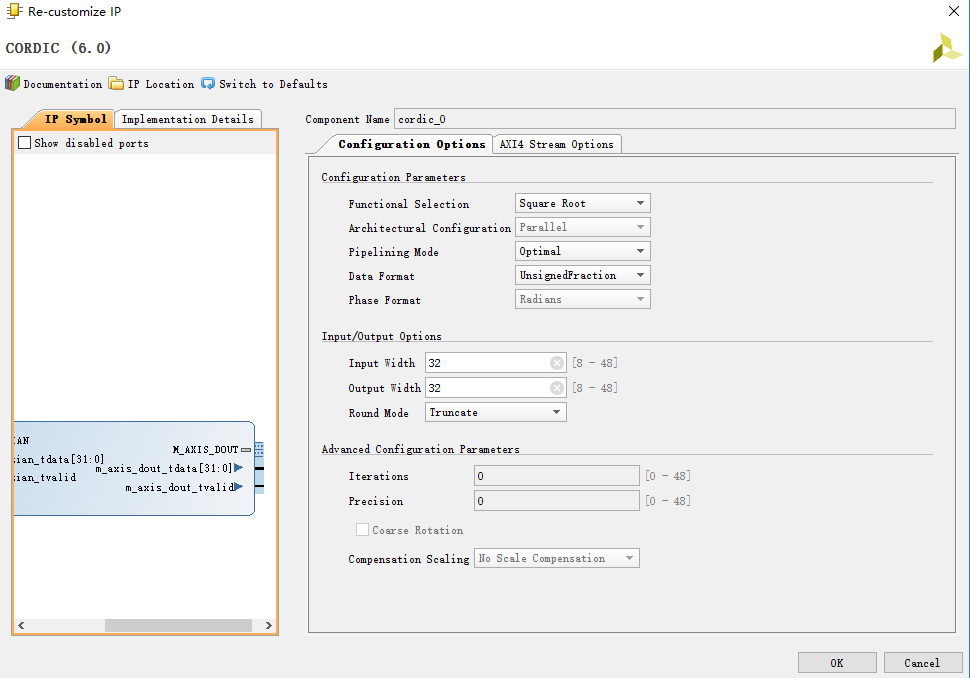
3.牛顿迭代忽略余数的实现方法

`timescale 1ns / 1ps
//////////////////////////////////////////////////////////////////////////////////
// Company:
// Engineer:
//
// Create Date: 2018/08/07 16:26:46
// Design Name:
// Module Name: sqrt
// Project Name:
// Target Devices:
// Tool Versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
//////////////////////////////////////////////////////////////////////////////////

module sqrt
    #(
            parameter                                       d_width = ,
            parameter                                   q_width = d_width/ - ,
            parameter                                   r_width = q_width +     )
    (
    input            wire                                    clk,
    input            wire                                    rst,
    input            wire                                    i_vaild,
    input            wire            [d_width-:]            data_i,//data_21,data_12,data_22, //输入

    output        reg                                    o_vaild,
    output        reg            [q_width:]            data_o, //输出
    output        reg            [r_width:]            data_r  //余数
    );

//--------------------------------------------------------------------------------

    reg                             [d_width-:]         D                [r_width:]; //被开方数
    reg                             [q_width:]         Q_z            [r_width:]; //临时
    reg                             [q_width:]         Q_q            [r_width:]; //确认
    reg                                                     ivalid_t        [r_width:];
//--------------------------------------------------------------------------------
    always@(posedge    clk or posedge    rst)
        begin
            if(rst)
                begin
                    D[r_width] <= ;
                    Q_z[r_width] <= ;
                    Q_q[r_width] <= ;
                    ivalid_t[r_width] <= ;
                end
            else    if(i_vaild)
                begin
                    D[r_width] <= data_i;//data_11+data_21+data_12+data_22;  //被开方数据
                    Q_z[r_width] <= {'b1,{q_width{1'b0}}}; //实验值设置
                    Q_q[r_width] <= ; //实际计算结果
                    ivalid_t[r_width] <= ;
                end
            else
                begin
                    D[r_width] <= ;
                    Q_z[r_width] <= ;
                    Q_q[r_width] <= ;
                    ivalid_t[r_width] <= ;
                end
        end
//-------------------------------------------------------------------------------

//        迭代计算过程

//-------------------------------------------------------------------------------
        generate
            genvar i;
                for(i=r_width-;i>=;i=i-)
                    begin:U
                        always@(posedge clk or posedge    rst)
                            begin
                                if(rst)
                                    begin
                                        D[i] <= ;
                                        Q_z[i] <= ;
                                        Q_q[i] <= ;
                                        ivalid_t[i] <= ;
                                    end
                                else    if(ivalid_t[i+])
                                    begin
                                        if(Q_z[i+]*Q_z[i+] > D[i+])
                                            begin
                                                Q_z[i] <= {Q_q[i+][q_width:i],'b1,{{i-1}{1'b0}}};
                                                Q_q[i] <= Q_q[i+];
                                            end
                                        else
                                            begin
                                                Q_z[i] <= {Q_z[i+][q_width:i],'b1,{{i-1}{1'b0}}};
                                                Q_q[i] <= Q_z[i+];
                                            end
                                        D[i] <= D[i+];
                                        ivalid_t[i] <= ;
                                    end
                                else
                                    begin
                                        ivalid_t[i] <= ;
                                        D[i] <= ;
                                        Q_q[i] <= ;
                                        Q_z[i] <= ;
                                    end
                            end
                    end
        endgenerate
//--------------------------------------------------------------------------------

//    计算余数与最终平方根

//--------------------------------------------------------------------------------
        always@(posedge    clk or posedge    rst)
            begin
                if(rst)
                    begin
                        data_o <= ;
                        data_r <= ;
                        o_vaild <= ;
                    end
                else    if(ivalid_t[])
                    begin
                        if(Q_z[]*Q_z[] > D[])
                            begin
                                data_o <= Q_q[];
                                data_r <= D[] - Q_q[]*Q_q[];
                                o_vaild <= ;
                            end
                        else
                            begin
                                data_o <= {Q_q[][q_width:],Q_z[][]};
                                data_r <= D[] - {Q_q[][q_width:],Q_z[][]}*{Q_q[][q_width:],Q_z[][]};
                                o_vaild <= ;
                            end
                    end
                else
                    begin
                        data_o <= ;
                        data_r <= ;
                        o_vaild <= ;
                    end
            end
//--------------------------------------------------------------------------------
endmodule

三种方法的精度对比以及资源占用情况

JPL近似

IPcordic使用：

牛顿迭代

可以看出资源占用：newtoon>JPL > IPcordic，精度的估计JPL<newtoon<IPcordic,

其中JPL 的计算速度快，但是误差太高了

单独求倒数的模块    /    快速高精度求平方根倒数的算法