Educational DP Contest E - Knapsack 2 (01背包进阶版)

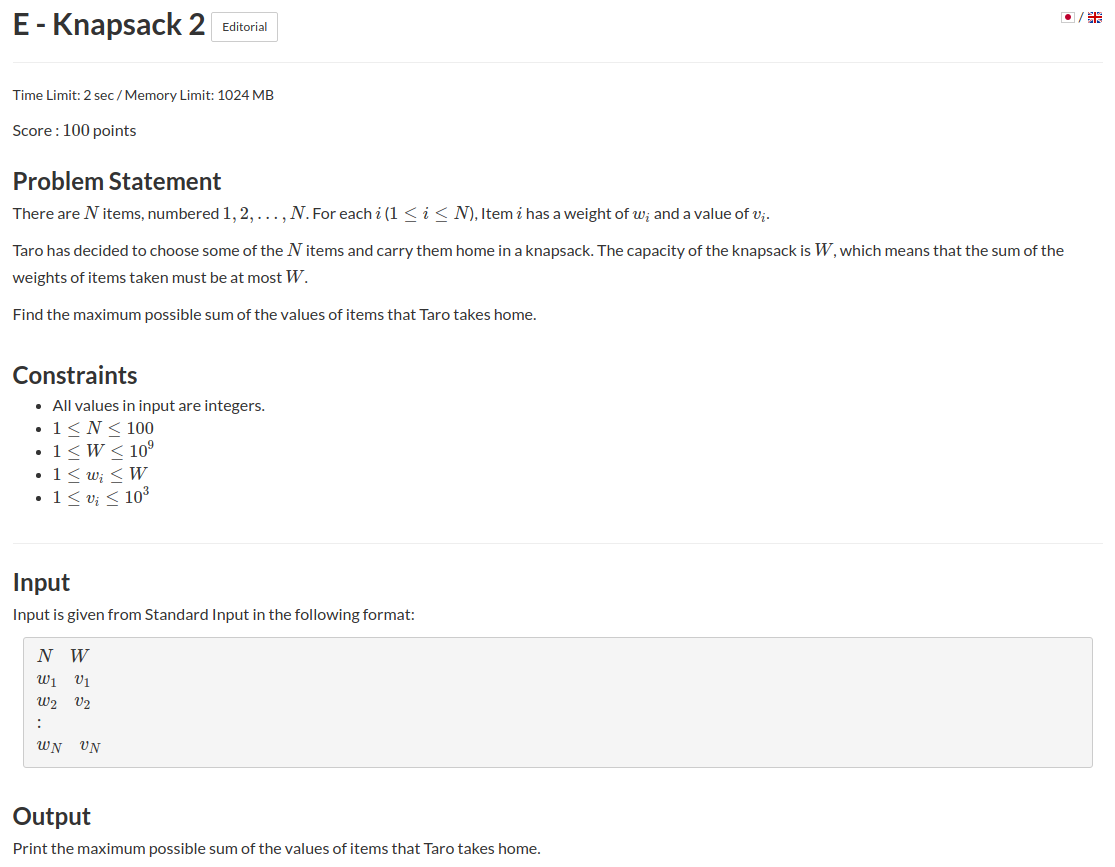
• 题意:有\(n\)个物品,第\(i\)个物品价值\(v_{i}\),体积为\(w_{i}\),你有容量为\(W\)的背包,求能放物品的最大价值.

• 题解:经典01背包,但是物品的最大体积给到了\(10^9\),dp数组下标会造成越界,因此我们不能用dp下标来存物品的体积,但是我们发现,物品的价值范围很小,所以我们反着想,枚举所有可能的总价值,dp数组下标表示可能的最大价值,值表示可能的最大的价值的最小体积,然后判断是否合法,维护最大价值.

• 代码:

  int n,W;
  int w[N],v[N];
  int dp[N];
  int main() {
      //ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  	n=read();
  	W=read();
  	me(dp,INF,sizeof(dp));
  	dp[0]=0;
  	for(int i=1;i<=n;++i){
  		w[i]=read();
  		v[i]=read();
  	}
  	int res=0;
  	for(int i=1;i<=n;++i){
  		for(int j=1e5;j>=v[i];--j){
  			dp[j]=min(dp[j],dp[j-v[i]]+w[i]);
  			if(dp[j]<=W) res=max(res,j);
  		}
      }
  	printf("%d\n",res);
      return 0;
  }