【模式识别与机器学习】——最大似然估计 （MLE） 最大后验概率（MAP）和最小二乘法

1） 极/最大似然估计 MLE

给定一堆数据，假如我们知道它是从某一种分布中随机取出来的，可是我们并不知道这个分布具体的参，即“模型已定，参数未知”。例如，我们知道这个分布是正态分布，但是不知道均值和方差；或者是二项分布，但是不知道均值。 最大似然估计（MLE，Maximum Likelihood Estimation）就可以用来估计模型的参数。MLE的目标是找出一组参数，使得模型产生出观测数据的概率最大：

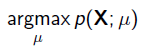
其中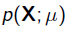就是似然函数，表示在参数下出现观测数据的概率。我们假设每个观测数据是独立的，那么有

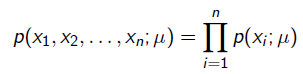
为了求导方便，一般对目标取log。 所以最优化对似然函数等同于最优化对数似然函数：

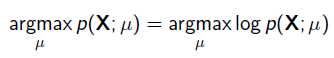
例子1：举一个抛硬币的简单例子。 现在有一个正反面不是很匀称的硬币，如果正面朝上记为H，方面朝上记为T，抛10次的结果如下：

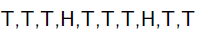
求这个硬币正面朝上的概率有多大？

很显然这个概率是0.2。现在我们用MLE的思想去求解它。我们知道每次抛硬币都是一次二项分布，设正面朝上的概率是，那么似然函数为：

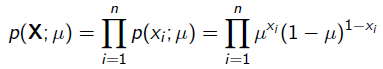
x=1表示正面朝上，x=0表示方面朝上。那么有：

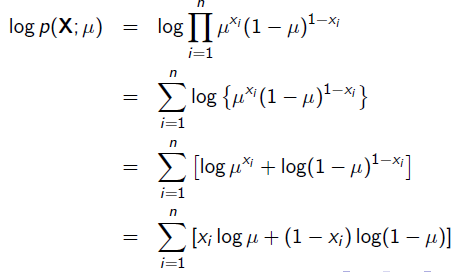
求导：

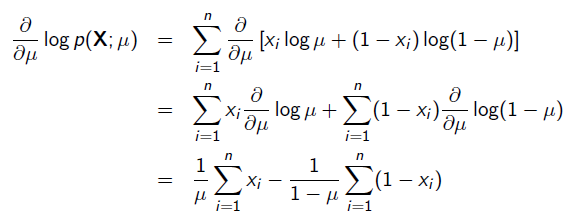
令导数为0，很容易得到：

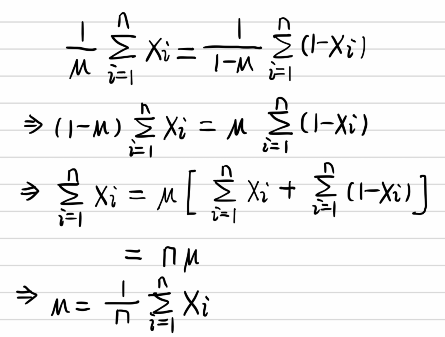
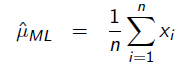
也就是0.2 。

总结一下：求极大似然函数估计值的一般步骤
（1） 写出似然函数； 
（2） 对似然函数取对数，并整理； 
（3） 求导数； 
（4） 解似然方程 。

例子2：假如一个盒子里面有红黑共10个球，每次有放回的取出，取了10次，结果为7次黑球，3次红球。问拿出黑球的概率 p 是多少？

我们假设7次黑球，3次红球为事件 A ，一个理所当然的想法就是既然事件 A已经发生了，那么事件 A 发生的概率应该最大。所以既然事件 A 的结果已定， 我们就有理由相信这不是一个偶然发生的事件，这个已发生的事件肯定一定程度上反映了黑球在整体中的比例。所以我们要让模型产生这个整体事件的概率最大，我们把这十次抽取看成一个整体事件 A ，很明显事件 A 发生的概率是每个子事件概率之积。我们把 P(A) 看成一个关于 p 的函数，求 P(A) 取最大值时的 p ，这就是极大似然估计的思想。具体公式化描述为P(A)=p^7*(1-p)^3。

接下来就是取对数转换为累加，然后通过求导令式子为0来求极值，求出p的结果。

MLE是频率学派模型参数估计的常用方法。

-顾名思义：似然，可以简单理解为概率、可能性，也就是说要最大化该事件发生的可能性

-根据已知样本，希望通过调整模型参数来使得模型能够最大化样本情况出现的概率。

（2）最大后验概率估计（MAP）

-是贝叶斯派模型参数估计的常用方法。

-顾名思义：就是最大化在给定数据样本的情况下模型参数的后验概率

-依然是根据已知样本，来通过调整模型参数使得模型能够产生该数据样本的概率最大，只不过对于模型参数有了一个先验假设，即模型参数可能满足某种分布，不再一味地依赖数据样例（万一数据量少或者数据不靠谱呢）。

例子1：在这里举个掷硬币的例子：抛一枚硬币10次，有10次正面朝上，0次反面朝上。问正面朝上的概率p。

在频率学派来看，利用极大似然估计可以得到 p= 10 / 10 = 1.0。显然当缺乏数据时MLE可能会产生严重的偏差。

如果我们利用极大后验概率估计来看这件事，先验认为大概率下这个硬币是均匀的 (例如最大值取在0.5处的Beta分布)，那么P(p|X)，是一个分布，最大值会介于0.5~1之间，而不是武断的给出p= 1。显然，随着数据量的增加，参数分布会更倾向于向数据靠拢，先验假设的影响会越来越小。

MAP优化的是一个后验概率，即给定了观测值后使概率最大：

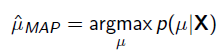
把上式根据贝叶斯公式展开：

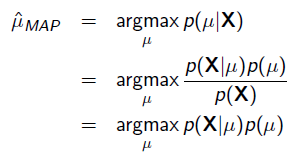
我们可以看出第一项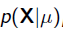就是似然函数，第二项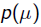就是参数的先验知识。取log之后就是：

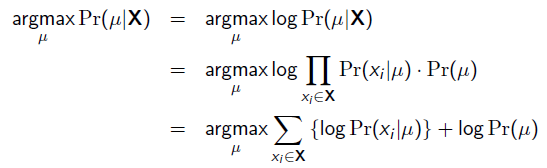
回到刚才的抛硬币例子，假设参数有一个先验估计，它服从Beta分布（见后），即：

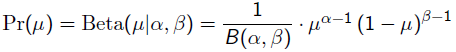
而每次抛硬币任然服从二项分布：

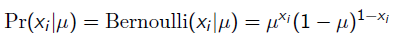
那么，目标函数的导数为：

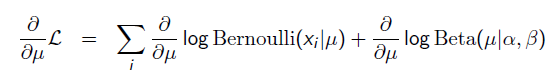
求导的第一项已经在上面MLE中给出了，第二项为：

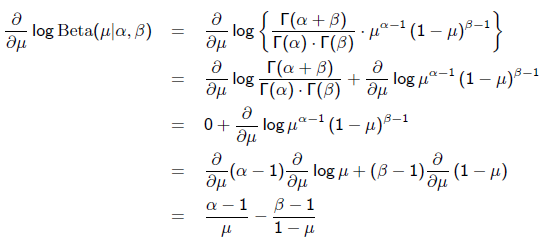
令导数为0，求解为：

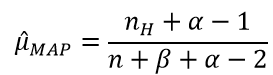
其中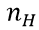，表示正面朝上的次数。这里看以看出，MLE与MAP的不同之处在于，MAP的结果多了一些先验分布的参数。

————————————————————————————————————

补充知识： Beta分布

Beat分布是一种常见的先验分布，它形状由两个参数控制，定义域为[0,1]

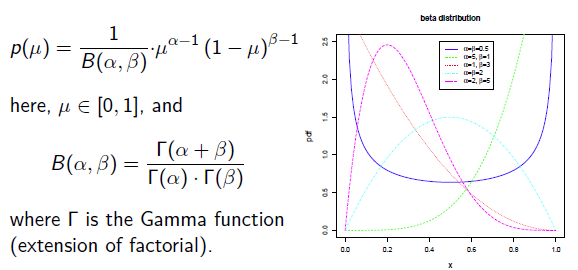
Beta分布的最大值是x等于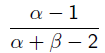的时候：

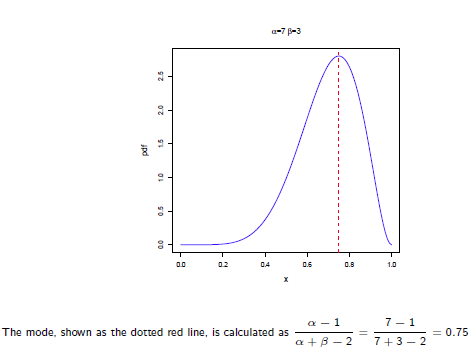
所以在抛硬币中，如果先验知识是说硬币是匀称的，那么就让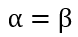。 但是很显然即使它们相等，它两的值也对最终结果很有影响。它两的值越大，表示偏离匀称的可能性越小：

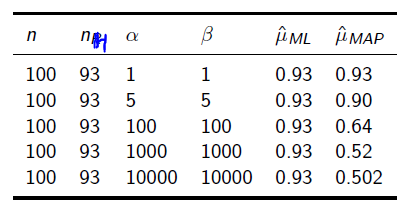
（3）MAP和MLE的区别和联系

极大后验估计(Maximum A Posterior, MAP)
上述最大似然估计有一个问题，就是没有考虑到模型本身的概率分布。
极大似然估计是求使得P(x|θ)取最大值的θ值，而极大后验概率是求使得P(x|θ)p(θ),即P(θ|x),取最大值的θθ值.
由贝叶斯定理：

最大似然估计可以理解为当先验概率P(θ)P(θ)为均匀分布时的极大后验估计器。极大后验估计根据经验数据获得对难以观察的量的点估计。与最大似然估计类似，但是最大的不同是，最大后验估计融入了要估计量的先验分布在其中，可看做是规则化的最大似然估计。

注：最大后验估计可以看做贝叶斯估计的一种特定形式。
MAP函数的求解和MLE函数的求解方法相同，都是先取对数，然后通过微分求解。MAP与MLE最大区别是MAP中加入了模型参数本身的概率分布，或者说。MLE中认为模型参数本身的概率的是均匀的，即该概率为一个固定值。

（4）最小二乘法

最小二乘法(Least Square) 

通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。

求解：多元函数求极值的方法，对θ求偏导，让偏导等于0，求出θ值。当θ为向量时，需要对各个θi求偏导计算。