【算法•日更•第二十八期】图论：强连通+Tarjan算法（一）

▎前言

　　一直都想学习这个东西，以为很难，结果发现也不过如此。

　　只要会些图论的基础就可以了。

▎强连通

☞『定义』

　　既然叫强连通，那么一定具有很强的连通性。

　　强连通：就是指在一个有向图中，两个顶点可以互相到达，那么我们就称之为强连通；

　　强连通图：在一个有向图中，任意两个点都可以互相到达，那么我们称这个图是一个强连通图；

　　强连通分量：在一个有向图中（不一定是强连通图），一定有很多子图是强连通图，特别的，单独的一个点也是强连通图，而强连通分量则是分成的最大的强连通图。

　　以下三个红框中的都是强连通分量：

　　

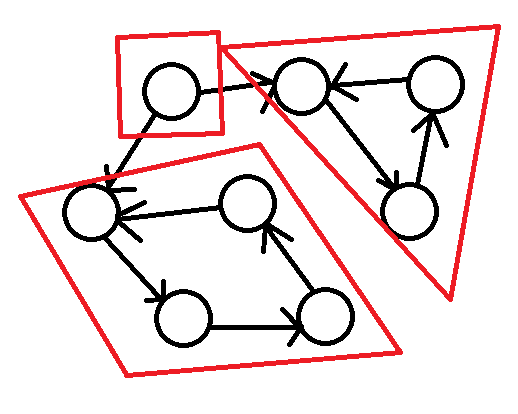
☞『dfs&有向图』

　　图的遍历如果使用dfs的话，就会形成一棵树的样子。

　　原理很简单，从任意一个顶点出发，不断扩展，已经遍历过的那么就不再遍历了，直到无法继续遍历（也可能有点会不连接）。

　　其中这棵树当前节点扩展出的边与这棵树之间有很多关系。

　　因此在了解了这些之后，我们还得弄清楚一些概念：

　　假设当前节点为u。

　　①树枝边：就是u所扩展出的边，且没有访问过；

　　②前向边：指向DFS树中子树中节点的边；

　　③后向边：指向DFS树中父亲的边；

　　④横叉边：指向DFS树中非子树的边。

☞『关系的判定』

　　首先规定一下：当前节点为u，扩展节点为v，low数组存储的是当前节点及其子树的离根节点最近的节点编号,dfn数组存储的是当前节点被访问的序号。

　　请看下面的图：

　　　　

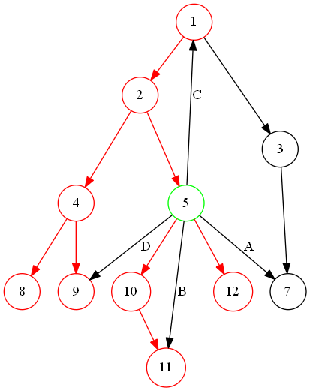
　　当前节点编号是5，那么：

　　①树枝边：A边还没有访问过，为树枝边；

　　②前向边：B边的dfn[v]>dfn[u]，说明在子树中，那么这是一条前向边；

　　③后向边：C边已经访问过了，不在子树中且在栈中，所以这是一条后向边；

　　④横叉边：D边已经访问过且不在子树中，且已经出栈，所以是一条横叉边。

▎Tarjan算法

☞『什么是Tarjan算法？』

　　一种由Robert Tarjan提出的求解有向图强连通分量的线性时间的算法。

　　Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。（copy自百度）

☞『算法核心』

　　对于一条边（u，v），我们在之前的讲解中已经提到了dfn和low数组的意思。

　　那么初始状态下：low[u]=dfn[u]，这应该很好想，初始状态下离根节点最近的节点编号先赋值为自己遍历的编号，和并查集的初始化类似。

　　每一次扩展时，若边为树枝边，那么我们就使用low[v]来更新low[u]，如果是后向边，那么我们就使用dfn[v]来更新。

　　当low[u] == dfn[u]时，就是一个分割点，要把u之后入栈的元素及u全部弹出栈。

　　可能有些难理解，推荐一篇别人的博客，图解画得很好，链接在此。

　　当然，问tarjan算法也会告诉你图解的，小编就不画了。