Andrew Ng 机器学习公开课 - 线性回归

我的机器学习系列从现在开始将会结合Andrew Ng老师与sklearn的api是实际应用相结合来写了。

吴恩达（1976-，英文名：Andrew Ng），华裔美国人，是斯坦福大学计算机科学系和电子工程系副教授，人工智能实验室主任。吴恩达是人工智能和机器学习领域国际上最权威的学者之一。吴恩达也是在线教育平台Coursera的联合创始人（with Daphne Koller）。

2014年5月16日，吴恩达加入百度，担任百度公司首席科学家，负责百度研究院的领导工作，尤其是Baidu Brain计划。

2017年10月，吴恩达将出任Woebot公司新任董事长，该公司拥有一款同名聊天机器人。

 

scikit-learn，基于SciPy，目前开发者们针对不同的应用领域已经发展出了为数众多的分支版本，它们被统一称为Scikits，即SciPy工具包的意思。而在这些分支版本中，最有名，也是专门面向机器学习的一个就是Scikit-learn。

Scikit-learn项目最早由数据科学家David Cournapeau 在2007 年发起，需要NumPy和SciPy等其他包的支持，是Python语言中专门针对机器学习应用而发展起来的一款开源框架。

它的维护也主要依靠开源社区。

-------------------------------------------正文-------------------------------------------------

在做数学分析之前我们需要掌握以下知识

1.矩阵求导

2.方阵的迹

1.矩阵求导：

　　设现在有一方程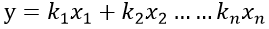可知y的值是受x1，x2... ... xn 的值变化，我们可以这么类比，在三维空间中存在一个平面，这个平面弯弯曲曲，在平面上的一点他的梯度由向x和y方向的下降的趋势组成，回到方程也就是说y的 y的导 由 沿着 x1 ......xn方向上的“斜率”叠加而成，那就显而易见了，我们就是要求出y的全微分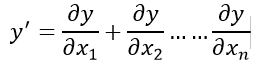，现在回到矩阵分析矩阵的。我们定义一个矩阵使得第一列的值为x1第二列的为x2一直到xn

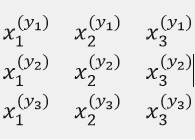
这张图片表示这三个y方程的数据，为了方便我只列了三个特征（也就是x）因为矩阵的每一行代表着一个y ，y对矩阵求导就有

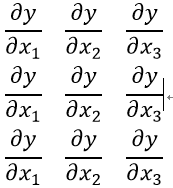
当然为这是为了让大家看清楚并且更能理解，更好的表示求偏导这一特性。

所以得出结论函数ff是从m∗nm∗n的矩阵到实数域的映射，对其求梯度可以表示为如下形式：

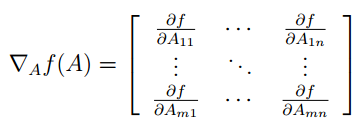
当然f(A)是矩阵等情况读者你就可以自己了解一下。

2.方阵的迹

定义：在线性代数中，一个n×n矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵A的迹（或迹数），一般记作tr(A)。于是就有

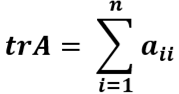
我们需要用到方阵的迹的几大性质

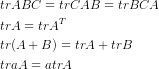
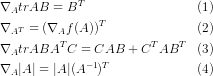
我对第一（1）进行了证明

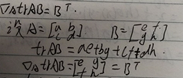
好到此为止我们需要整理的线性代数的知识就到此为止了。

问题提出

现在有这么一组数据每一行为一个样本。我们把样本中房子的价格称作features，把卧室数目和房子大小称作target。也就是说在这组数据中每一个样本有两个target和一个features，这个features就是我们要预测出的答案，也就好比方程y=ax1+bx2+C

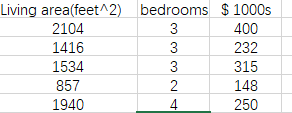
我们先定义一些符号

m = training examples

x = "input" variables features

y = "output"variable target

(x,y) - training example

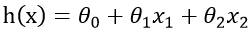
有时我们需要让假设h对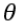的依赖表示出来并且我们假设x0 = 1。

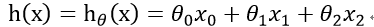
为了让式子更加简洁

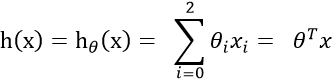
此时我们使用最小二乘法来表示算出来的结果与正实数据的关系

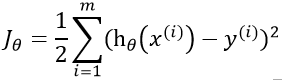
注：1/2 是为了更好的计算后面就知道了。

现在我们的任务为找到一组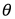使得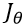最小最好越接近于0越好，越接近0代表数据越线性。

接下来我们来了解一个关于梯度的知识

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

所以当我们在沿着梯度的方向下降的时候是下降的最快的，当我们的梯度下降到最低为什么是梯度为零时结束 呢？
当迭代点是最优时，其对应的梯度为零称之为无约束问题解得一阶必要条件 
证明的核心思想是利用最优点处利用泰勒展开，因为已经是最优点，所以在其附近的点函数值近似相等，便可以得到梯度为零的结论

所以我们可以写出迭代方程

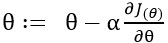
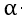是步长，也就是你朝着梯度的方向下山一步迈远。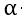过小会导致迭代时间太长。过大可以越过最低点，导致来回震荡，这里的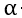是需要我们手动输入的

1.第一种解法（迭代少）

对式子的每一行为更新一次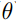求出结果为

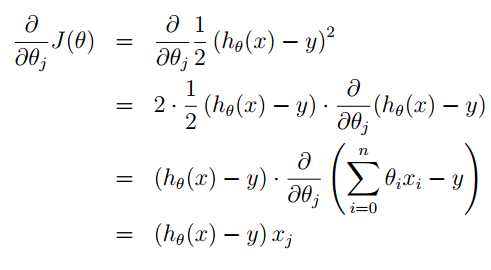
则此时迭代方程为

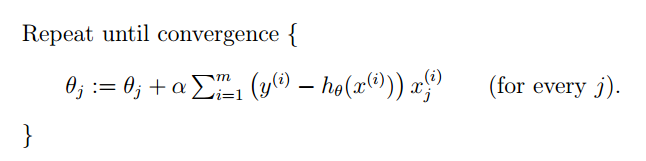
此时我们是根据第一个样本修改后在来修改第二个参数每一行为一个样本进行迭代。我们画一个等高线，此时的下降趋势为

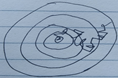
可以看到随意每次的方向有弯路但是大体方向还是走到了最低处。

2.正规方程

正规方程每次迭代更新需要整个矩阵的数据来求出。

现在我们每一个样本的数据都设置为列矩阵通过下面这种方式来将我们的target examples来表示出来自然 y用来表示features examples。

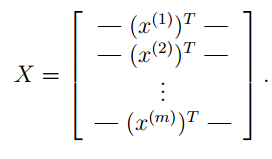
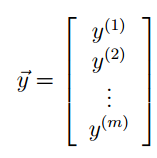
此时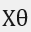为

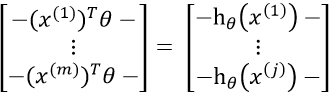
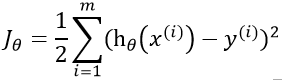
因为

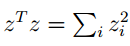
根据我们上面对矩阵的迹和求导就可得

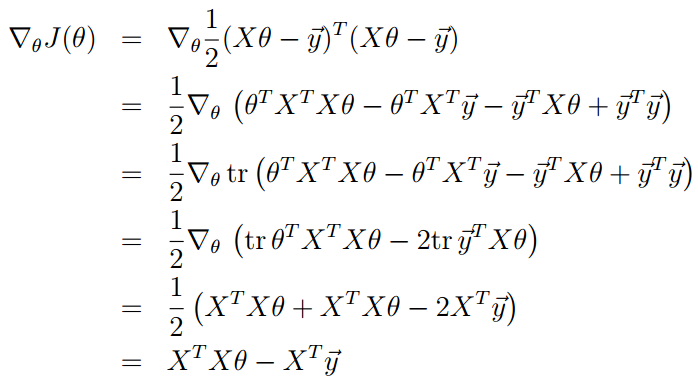
得出最优解

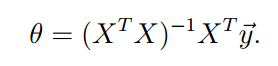
参考文献：

1、斯坦福大学公开课 机器学习

　　讲师：吴恩达 （Andrew Ng）

　　原视频：http://open.163.com/special/opencourse/machinelearning.html

2、Scikit-Learn简介

　　作者：yoyofu007 　
　　来源：CSDN 
　　原文：https://blog.csdn.net/yoyofu007/article/details/80924166