Codeforces Round #450 (Div. 2) ABCD

这次还是能看的0 0，没出现一题掉分情况。

QAQ前两次掉分还被hack了0 0,两行清泪。

A. Find Extra One

 

You have n distinct points on a plane, none of them lie on OY axis. Check that there is a point after removal of which the remaining points are located on one side of the OY axis.

Input

The first line contains a single positive integer n (2 ≤ n ≤ 105).

The following n lines contain coordinates of the points. The i-th of these lines contains two single integers xi and yi (|xi|, |yi| ≤ 109,xi ≠ 0). No two points coincide.

Output

Print "Yes" if there is such a point, "No" — otherwise.

You can print every letter in any case (upper or lower).

Examples

input

3
1 1
-1 -1
2 -1

output

Yes

input

4
1 1
2 2
-1 1
-2 2

output

No

input

3
1 2
2 1
4 60

output

Yes

---

题意：给你n个平面上的点，能否去掉一个使得所有点在y轴一侧。给出的点不会在y轴上。

题解：水题，统计下x>0 和 x<0的数字个数就好了。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define mod 1000000007
 #define LL long long
 #define INF 0x3f3f3f3f
 using namespace std;
 int main()
 {
     int n,left,right,x,y;
     left=right=;
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         scanf("%d%d",&x,&y);
         if(x>)
             right++;
         else
             left++;
     }
     if(right<= || left<=)
         printf("Yes\n");
     else
         printf("No\n");
     return ;
 }

B. Position in Fraction

 

You have a fraction . You need to find the first occurrence of digit c into decimal notation of the fraction after decimal point.

Input

The first contains three single positive integers a, b, c (1 ≤ a < b ≤ 105, 0 ≤ c ≤ 9).

Output

Print position of the first occurrence of digit c into the fraction. Positions are numbered from 1 after decimal point. It there is no such position, print -1.

Examples

input

1 2 0

output

2

input

2 3 7

output

-1

---

题意：给出一个分数$ \frac{a}{b} $ ，看c在该分数小数点后几位。

题解：$ \frac{a}{b} $化为最简$ \frac{a'}{b'} $后，我们模拟除法列竖式求答案的过程。由于列竖式的过程中余下的数总比b'小，所以最多b'个不同余数，列竖式的过程中一旦出现相同的余数则是进入了循环。所以我们最多做b'次除法就能求出c是否存在于该分数小数点后以及c的位置。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define mod 1000000007
 #define LL long long
 #define INF 0x3f3f3f3f
 using namespace std;
 int gcd(int a,int b)
 {
     int c;
     while(b)
     {
         c=a%b;
         a=b;
         b=c;
     }
     return a;
 }
 int main()
 {
     int a,b,c,d,e,i;
     scanf("%d%d%d",&a,&b,&c);
     d=gcd(a,b);
     a/=d;
     b/=d;
     d=a/b;
     a-=d*b;
     a*=;
     for(i=;i<=;i++)
     {
         d=a/b;
         a-=d*b;
         if(d==c)
             break;
         a*=;
     }
     if(i>)
         printf("-1\n");
     else
         printf("%d\n",i);
     return ;
 }

C. Remove Extra One

 

You are given a permutation p of length n. Remove one element from permutation to make the number of records the maximum possible.

We remind that in a sequence of numbers a1, a2, ..., ak the element ai is a record if for every integer j (1 ≤ j < i) the following holds:aj < ai.

Input

The first line contains the only integer n (1 ≤ n ≤ 105) — the length of the permutation.

The second line contains n integers p1, p2, ..., pn (1 ≤ pi ≤ n) — the permutation. All the integers are distinct.

Output

Print the only integer — the element that should be removed to make the number of records the maximum possible. If there are multiple such elements, print the smallest one.

Examples

input

1
1

output

1

input

5
5 1 2 3 4

output

5

Note

In the first example the only element can be removed.

---

题意:给出1~n的一个排列，要求你找出一个数，在排列中去掉它以后符合条件的数最多，如果有多个则选最小的那个。若ai符合条件，对于任意1≤j<i，aj<a_i。

题解：那么我们写个bit来记录数列前面小于ai的个数，set来求取大于ai的第一个数。如果ai前面有i-2个数小于ai，那么用set的lonwer_bound找到大于a_i的第一个数p，并且该数p对于答案的贡献num[p]++。注意如果ai前面有i-1个数小于a_i，那么a_i对于答案的贡献num[a_i]--。然后从小到大找贡献最大的那个。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define mod 1000000007
 #define LL long long
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=1e5+;
 int bits[N];
 int num[N];
 int n,m,T,k,p;
 set<int> pt;
 set<int>::iterator it;
 void add(int i,int x)
 {
     while(i<=n)
     {
         bits[i]+=x;
         i+=(i &(-i));
     }
     return ;
 }
 int sum(int i)
 {
     int res=;
     while(i>)
     {
         res+=bits[i];
         i-=(i &(-i));
     }
     return res;
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         scanf("%d",&p);
         if((p-> && sum(p-)==i-) || (p-== && i==))
         {
             it=pt.lower_bound(p);
             num[*it]++;
         }
         if((p-> && sum(p-)==i-) || (p-== && i==))
             num[p]--;
         pt.insert(p);
         add(p,);
     }
     int maxn=num[];
     k=;
     for(int i=;i<=n;i++)
     {
         if(maxn<num[i])
         {
             maxn=num[i];
             k=i;
         }
     }
     printf("%d\n",k);
     return ;
 }

D. Unusual Sequences

 

Count the number of distinct sequences a1, a2, ..., an (1 ≤ ai) consisting of positive integers such that gcd(a1, a2, ..., an) = x and 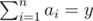. As this number could be large, print the answer modulo 109 + 7.

gcd here means the greatest common divisor.

Input

The only line contains two positive integers x and y (1 ≤ x, y ≤ 109).

Output

Print the number of such sequences modulo 109 + 7.

Examples

input

3 9

output

3

input

5 8

output

0

---

题意：让你找出符合条件的序列数，并mod 1e9+7。序列需满足gcd（a_1~n）=x,sum(a_1~n）=y。

题解：首先把一个数p分解成几个数成组成的序列有$ 2^{p-1} $，用组合的隔板法轻易可证。x能整除y说明存在这样的序列，反之不存在。然后d=y/x，将d分解成质数乘积，算算不同质数的个数以及具体是哪些质数，容斥一下就能求出答案了。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define mod 1000000007
 #define LL long long
 #define INF 0x3f3f3f3f
 using namespace std;
 const int N=1e5+;
 int prime[N],inf[N],pcnt;
 void primer(int n)
 {
     pcnt=;
     for(int i=;i<=n;i++)
     {
         if(!inf[i])
         {
             prime[++pcnt]=i;
         }
         for(int j=;j<=pcnt;j++)
         {
             if(prime[j]>n/i) break;
             inf[prime[j]*i]=;
             if(i%prime[j]==) break;
         }
     }
     return ;
 }
 LL quick_pow(LL x,LL n)
 {
     LL res=;
     while(n)
     {
         if(n&)
             res=(res*x)%mod;
         n>>=;
         x=(x*x)%mod;
     }
     return res;
 }
 LL  x,y,d,n,k;
 int all;
 LL num[];
 int cnt;
 LL ans,p;
 int main()
 {
     primer();
     scanf("%lld%lld",&x,&y);
     if(y%x!=)
     {
         printf("0\n");
         return ;
     }
     y/=x;
     d=y;
     cnt=;
     for(int i=;(LL)prime[i]*prime[i]<=d;i++)
     {
         n=(LL)prime[i];
         if(d%n==)
         {
             num[++cnt]=n;
             while(d%n==) d/=n;
         }
     }
     if(d!=) num[++cnt]=d;
     ans=;
     all=(<<cnt)-;
     for(int i=,j,k,ok;i<=all;i++)
     {
         j=i;
         k=;
         p=;
         ok=;
         while(j)
         {
             k++;
             if(j&) p*=num[k],ok=-ok;
             j>>=;
         }
         ans=(ans+quick_pow(,y/p-)*ok)%mod;
     }
     printf("%lld\n",(ans%mod+mod)%mod);
     return ;
 }