leetcode 69 x 的平方根 牛顿迭代法

简介

简单的题, 直接上代码.

其实还挺复杂的.

参考链接

https://leetcode-cn.com/problems/sqrtx/solution/x-de-ping-fang-gen-by-leetcode-solution/

code

class Solution {
public:
    int mySqrt(int x) {
        return sqrt(x);
    }
};

class Solution {
    public int mySqrt(int x) {
        return (int)Math.sqrt(x);
    }
}

袖珍计算器法

其实是数学推导, 其实我还没怎么用过exp来进行计算和log

\[\sqrt{x} = x^{1/2} = (e ^ {\ln x})^{1/2} = e^{\frac{1}{2} \ln x}
\]

class Solution {
public:
    int mySqrt(int x) {
        if(x == 0) {
            return 0;
        }
        int ans = exp(0.5 * log(x));
        return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
    }
};

二分查找

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long long)mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
};

牛顿法

牛顿迭代法本质上是使用了泰勒级数的思想, 不过, 我不是特别清楚. 但是, 看了图片, 可知还是比较清晰的. 可以看参考链接

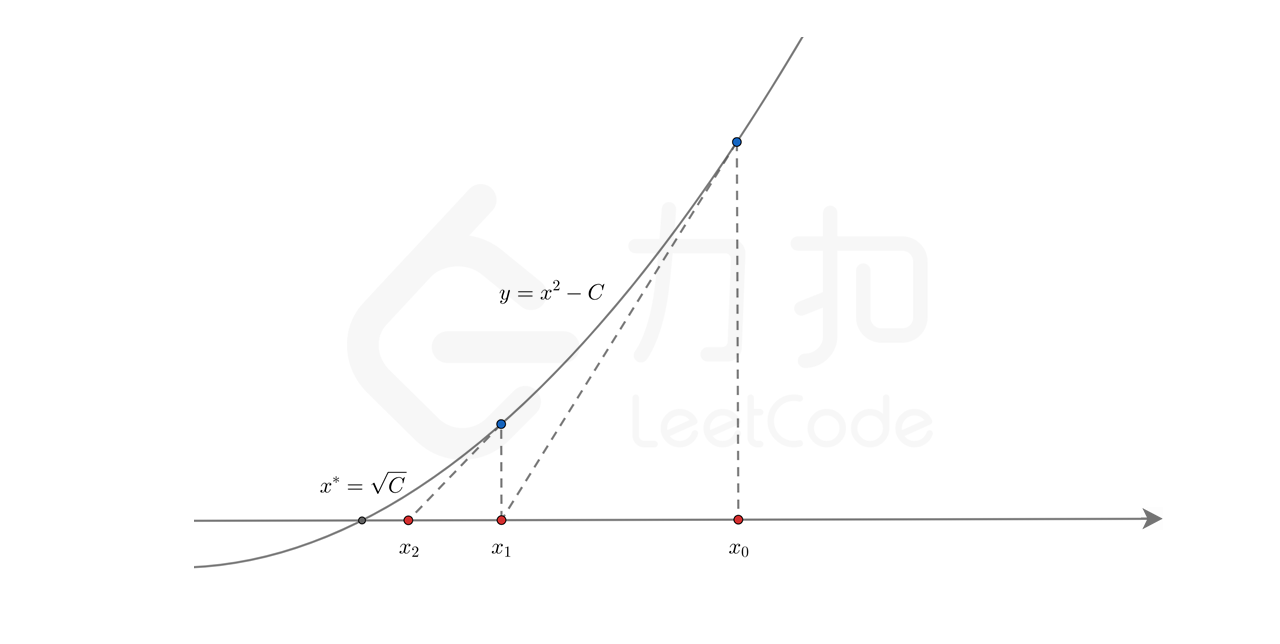
看了代码我们有了更深刻的理解

其实我们构建了一个函数

\[f(x) = x^2 - C
\]

其中\(C\)的初值设定为 输入的数 \(x_0\)

如果要这个方程\(f(x_0) == 0\) 的话, 其解 \(x_{解} = \sqrt{x_0}\)

然后我们又构建了一个直线函数求\(f(x)\)求导后的直线与\(y = 0\)的交点, 当两次的点的变化很接近的时候,就是我们想要的解的范围.

class Solution {
public:
    int mySqrt(int x) {
        if(x == 0) {
            return 0;
        }
        double C = x, x0 = x;
        while(true){
            double xi = 0.5 * (x0 + C/x0);
            if(fabs(x0 - xi) < 1e-7){
                break;
            }
            x0 = xi;
        }
        return int(x0);
    }
};