findHomography()函数详解

indHomography： 计算多个二维点对之间的最优单映射变换矩阵 H（3行x3列） ，使用最小均方误差或者RANSAC方法

函数功能：找到两个平面之间的转换矩阵。

Mat cv::findHomography    (    InputArray     srcPoints,
                                InputArray     dstPoints,
                                int     method = 0,
                                double     ransacReprojThreshold = 3,
                                OutputArray     mask = noArray(),
                                const int     maxIters = 2000,
                                const double     confidence = 0.995
)

参数详解：

srcPoints 源平面中点的坐标矩阵，可以是CV_32FC2类型，也可以是vector<Point2f>类型
dstPoints 目标平面中点的坐标矩阵，可以是CV_32FC2类型，也可以是vector<Point2f>类型
method 计算单应矩阵所使用的方法。不同的方法对应不同的参数，具体如下：
0 - 利用所有点的常规方法
RANSAC - RANSAC-基于RANSAC的鲁棒算法
LMEDS - 最小中值鲁棒算法
RHO - PROSAC-基于PROSAC的鲁棒算法
ransacReprojThreshold
将点对视为内点的最大允许重投影错误阈值（仅用于RANSAC和RHO方法）。如果

则点被认为是个外点（即错误匹配点对）。若srcPoints和dstPoints是以像素为单位的，则该参数通常设置在1到10的范围内。

mask
可选输出掩码矩阵，通常由鲁棒算法（RANSAC或LMEDS）设置。 请注意，输入掩码矩阵是不需要设置的。

maxIters RANSAC算法的最大迭代次数，默认值为2000。
confidence 可信度值，取值范围为0到1.
该函数能够找到并返回源平面和目标平面之间的转换矩阵H，以便于反向投影错误率达到最小。

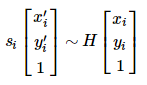
反向投影错误率计算方式如下：

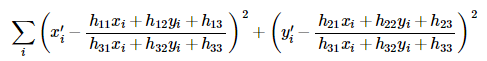
如果方法参数的值为默认值0，则该函数使用所有点对来计算具有简单最小二乘的初始单应性估计。

但是，如果不是所有的点对（srcPointsi，dstPointsi）都适合刚性透视变换（也就是说，存在一些外点（匹配错误点对）），那么这个初始估计就会很差。 在这种情况下，您可以使用三种鲁棒方法之一。 RANSAC，LMeDS和RHO等算法尝试对应点对（每对四对）的许多不同随机子集，使用该子集和简单最小二乘算法估计单应矩阵，然后计算计算单应性的质量/良好性（对于RANSAC来说，单应性的质量是指内点的数量，对于LMeDs来说，单应性的质量是指中值重投影的误差）。 最后，使用最佳子集来产生单应矩阵的初始估计和内点/异常值的掩模。

无论计算方法是否具有鲁棒性，计算单应矩阵都使用Levenberg-Marquardt方法进行细化（仅在鲁棒方法的情况下使用内点），以进一步减少重投影误差。

RANSAC和RHO方法几乎可以处理任何外点比例，但需要一个阈值来区分内点和外点。 LMeDS算法不需要任何阈值，但只有在超过50％的内点时它才能正常工作。 最后，如果没有外点且噪声很小，请使用默认方法（method = 0）。

该函数用于查找初始内部和外部矩阵。单应矩阵按比例确定。 因此，将其归一化以使。 若无法估计H矩阵，都会返回一个空矩阵。

方式二：

Mat cv::findHomography    (    InputArray     srcPoints,
                                InputArray     dstPoints,
                                OutputArray     mask,
                                int     method = 0,
                                double     ransacReprojThreshold = 3
)        

这是一个重载的成员函数，主要是为了方便使用而提出的。 它与上述函数的不同之处仅在于它接受的参数。

参考网址：Camera Calibration and 3D Reconstruction