.NET 模拟&编辑平滑曲线

本文介绍不依赖贝塞尔曲线，如何绘制一条平滑曲线，用于解决无贝塞尔控制点的情况下绘制曲线、但数据点不在贝塞尔曲线的场景。

在上一家公司我做过一个平滑曲线编辑工具，用于轮椅调整加减速曲线。基于几个用户可控制的点，生成一条平滑的曲线，控制点需要保持在曲线上。

今天和小伙伴沟通，白板的形状绘制笔迹，也可以使用到这个技术，所以需要回顾总结下

贝塞尔平滑曲线

我们先讲贝塞尔曲线GDI+ 中的贝塞尔自由绘制曲线 - Windows Forms .NET Framework | Microsoft Learn。一般情况我们绘制平滑曲线，直接以贝塞尔曲线API将多个点作为参数，直接进行绘制。这种情况下API会自动将第一个点作为控制点，得到贝塞尔曲线，比如下面生成一条平滑Geometry：

 1     var geometryTest = new StreamGeometry();
 2     using(var ctx = geometryTest.Open())
 3     {
 4         ctx.BeginFigure(_points[0], true, false);
 5         if(keyPoints.Count % 2 == 0)
 6         {
 7             //绘制二阶贝塞尔函数，需要保证为偶数点
 8             ctx.PolyQuadraticBezierTo(keyPoints, true, true);
 9         }
10         else
11         {
12             //绘制二阶贝塞尔函数，需要保证为偶数点
13             keyPoints.Insert(0, keyPoints[0]);
14             ctx.PolyQuadraticBezierTo(keyPoints, true, true);
15         }
16     }

这里的PolyQuadraticBezierTo函数，塞点集列表进去并设置平滑参数isSmoothJoin=true

1     public abstract void PolyQuadraticBezierTo(
2       IList<Point> points,
3       bool isStroked,
4       bool isSmoothJoin);
5
6     public abstract void PolyBezierTo(IList<Point> points, bool isStroked, bool isSmoothJoin);

官网有介绍，列表中第一个点作为控制点：StreamGeometryContext.PolyQuadraticBezierTo 方法 （System.Windows.Media） |Microsoft 学习

上面是自动设置控制点，这类实现方案会有一个问题：数据点最终可能不在曲线上

基于贝塞尔曲线，我们也可以计算控制点。但计算控制点，也是同样无法保证原始数据点会在拟合后的曲线上。

模拟平滑曲线

以现有数据点，如果直接相连肯定只会生成多个折线。如果我们添加多个点，可以模拟一条类似曲线路径的多边形近似点集，与Geometry下的FlattenedPathGeometry有点类似。

方案一，可以使用MathNet.Numerics生成一条X方向的N阶曲线，然后输入X坐标输出Y坐标，得到曲线上的点。 MathNet.Numerics可以参考 .NET 白板书写加速-曲线拟合预测 - 唐宋元明清2188 - 博客园。但这方案会生成无数点，曲线绘制性能无法得到保证。所以添加这些曲线路径的点，如何以最小的点集实现？可以对相邻点，对向量角度变化以及相邻间距设置一个最小阈值，最终得到符合的点集

方案二，用我之前实现方案，根据最简多项式代码算出近似样条曲线点集。原理同MathNet.Numerics里的Polynomial函数，下面是部分代码：

 1     private const double Tolerance = 0.5;
 2
 3     /// <summary>
 4     /// 获取拟合后的点集
 5     /// </summary>
 6     /// <param name="points"></param>
 7     /// <returns></returns>
 8     public static List<Point> GetFittingLinePoints(List<Point> points)
 9     {
10         var orderedPoints = (from pt in points orderby pt.X select pt).ToList();
11         var secondDerivatives = SecondDerivativeHelper.GetSecondDerivatives(orderedPoints);
12         List<Point> polyLinePoints = PointFakeApproximationHelper.GetSplinePolyLineApproximation(orderedPoints, secondDerivatives, Tolerance);
13         return polyLinePoints;
14     }

获取俩点之间点集：

 1         /// <summary>
 2         /// 用折线逼近三次多项式并给出公差。
 3         /// </summary>
 4         /// <param name="leftPoint">三次多项式左点</param>
 5         /// <param name="rightPoint">三次多项式右点</param>
 6         /// <param name="secondDerivativeLeft">左点三次多项式二阶导数.</param>
 7         /// <param name="secondDerivativeRight">右端三次多项式二阶导数.</param>
 8         /// <param name="tolerance">公差，即样条到近似折线的最大距离。</param>
 9         /// <returns>在给定公差的情况下逼近三次多项式的多边形点的列表。</returns>
10         private static Collection<Point> GetApproximation(Point leftPoint, Point rightPoint, double secondDerivativeLeft, double secondDerivativeRight, double tolerance)
11         {
12             // 左右俩点的X、Y轴值
13             double leftPointX = leftPoint.X, rightPointX = rightPoint.X;
14             double leftPointY = leftPoint.Y, rightPointY = rightPoint.Y;
15             // 次区间多项式系数
16             double a = (secondDerivativeRight - secondDerivativeLeft) / (6 * (rightPointX - leftPointX));
17             double b = (secondDerivativeLeft - 6 * a * leftPointX) / 2;
18             double c = (rightPointY - rightPointX * rightPointX * (a * rightPointX + b) - leftPointY + leftPointX * leftPointX * (a * leftPointX + b)) / (rightPointX - leftPointX);
19             double d = leftPointY - leftPointX * (leftPointX * (a * leftPointX + b) + c);
20
21             //如果a的值为0，则给a赋值double类型的最小正数
22             if(a == 0)
23                 a = double.Epsilon;
24
25             //通过多项式与拆线的逼近，获取多边形点的列表
26             Collection<Point> points = CubicPolynomialPolylineApproximation.Approximate(new Polynomial(new double[] { d, c, b, a }), leftPointX, rightPointX, tolerance);
27             return points;
28         }

效果如下图，左侧是原数据点集（绿色），右则截图是模拟后的点集显示（红色）：

 

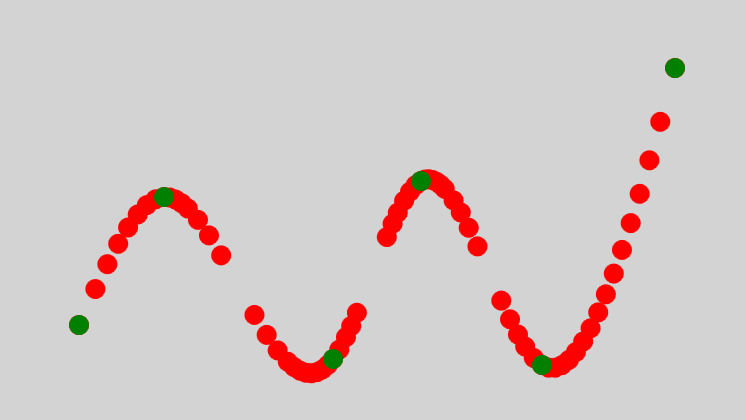
把这些新增点与原数据点，用直接连接起来，就是一条比较平滑的曲线了。同时原数据点也在拟合的曲线上。另外，如果还需要优化下这些线段的平滑，可以使用贝塞尔曲线替换直线连接，已经加了很多密集点，绿点不会脱离曲线的。

Github仓库代码 GitHub - kybs00/CurveLineEditDemo: 平滑曲线模拟及编辑Demo

编辑平滑曲线

上面我们已经完成了平滑曲线的点集模拟，连接起来就是一条曲线。在一些业务场景中，需要以曲线上的点为控制操作点，移动点以达到编辑曲线。

在曲线上设置多个操作点。如何在曲线上设置期望位置的点，可以看 .NET 曲线上的点- 获取距离最近的点 - 唐宋元明清2188 - 博客园。点击时，获取曲线离点击位置最近的点即可

选择点后，操作控制点移动。曲线根据操作点的位置变更，重新生成新的曲线。曲线编辑效果如下图：

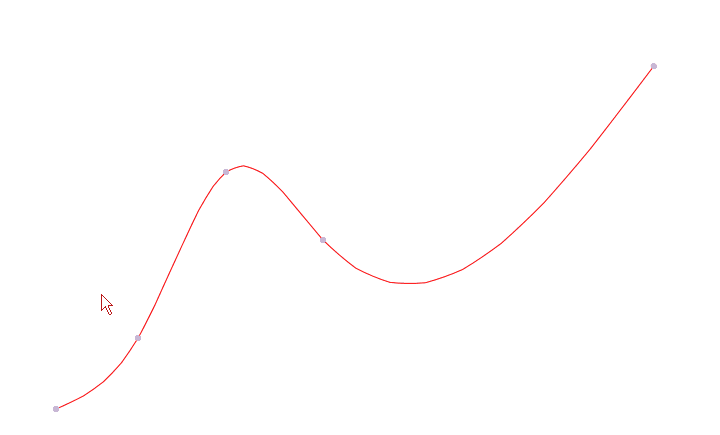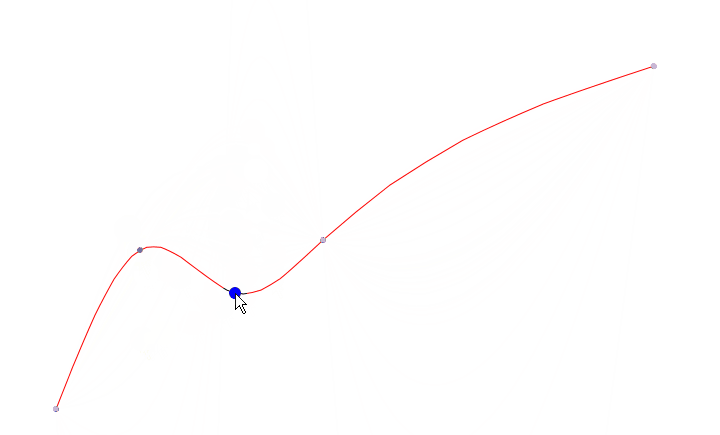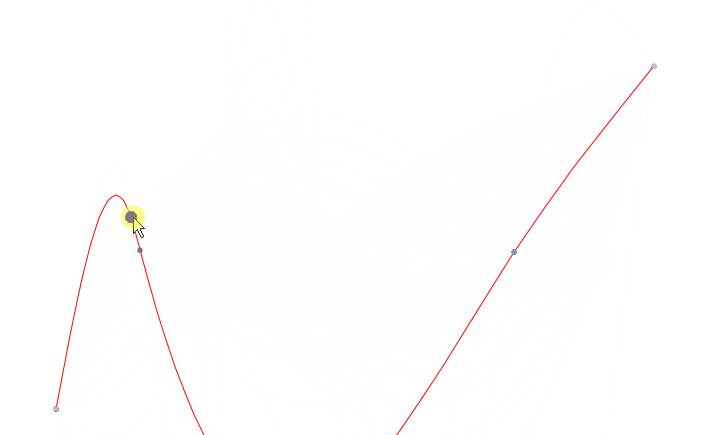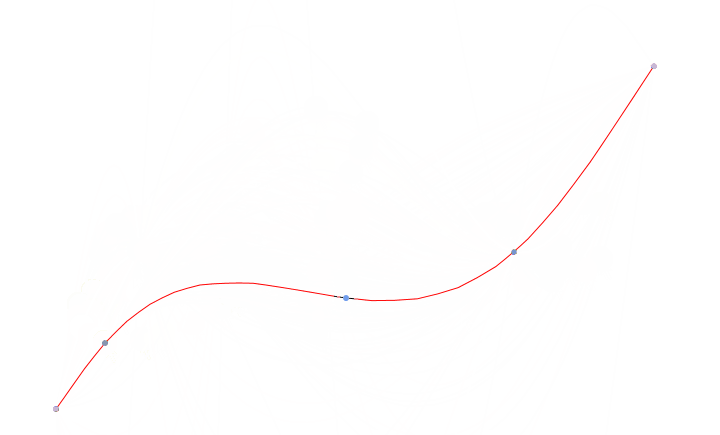
重新生成曲线这部分代码没有啥难点，核心代码就是上面的平滑曲线模拟。看上面仓库代码即可

参考文章：

GDI+ 中的贝塞尔自由绘制曲线 - Windows Forms .NET Framework | Microsoft Learn

Bezier曲线反求控制点_如何反求贝塞尔曲线的控制点-CSDN博客