skip list

概述

Skip list是平衡树的一种替代的数据结构，但是和红黑树不相同的是，跳表对于树的平衡的实现是基于一种随机化的算法的，这样也就是说跳表的插入和删除的工作是比较简单的。并且是Redis、LevelDB、nessDB、SkipDB等的底层结构，学习skip list为后面学习levelDB打下基础。

核心思想

如果是一个简单的链表，如图1，那么我们知道在链表中查找一个元素I的话，需要将整个链表遍历一次。

图 1

如果是说链表是排序的，并且节点中还存储了指向前面第二个节点的指针的话，如图2，那么在查找一个节点时，仅仅需要遍历N/2个节点即可。

图 2

这基本上就是跳表的核心思想，其实也是一种通过“空间来换取时间”的一个算法，通过在每个节点中增加了向前的指针，从而提升查找的效率。

跳表数据存储模型

我们定义：

如果一个基点存在k个向前的指针的话，那么陈该节点是k层的节点。

一个跳表的层MaxLevel定义为跳表中所有节点中最大的层数。

下面给出一个完整的跳表的图示：

那么我们该如何将该数据结构使用二进制存储呢？通过上面的跳表的很容易设计这样的数据结构：

定义每个节点类型：

typedef struct NodeStructure *Node;

typedef struct NodeStructure

{

keyType key; // key值

valueType value; // value值

// 向前指针数组，根据该节点层数的不同指向不同大小的数组

NodeStructure *forward[1];

}NodeStructure;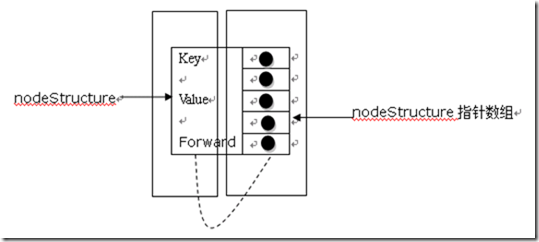

上面的每个结构体对应着图中的每个节点，如果一个节点是一层的节点的话（如7，12等节点），那么对应的forward将指向一个只含一个元素的数组，以此类推。

定义跳表数据类型：

// 定义跳表数据类型

typedef struct SkipList{

int level;  /* Maximum level of the list

(1 more than the number of levels in the list) */

Node header; /* pointer to header */

} * SkipList;跳表数据类型中包含了维护跳表的必要信息，level表明跳表的层数，header如下所示：

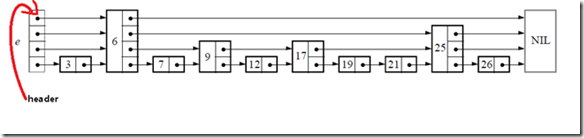
定义辅助变量：

#define MAX_LEVEL 10

定义辅助方法：

创建节点

Node CreateNode(int level,int key,int value)

{

Node node=(NodeStructure *)malloc(sizeof(NodeStructure)+level*sizeof(NodeStructure*));

node->key=key;

node->value=value;

return node;

}

好的基本的数据结构定义已经完成，接下来来分析对于跳表的一个操作。

跳表代码实现

1 初始化

初始化的过程很简单，仅仅是生成下图中红线区域内的部分，也就是跳表的基础结构：

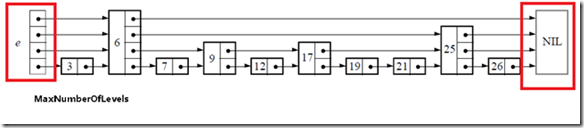
SkipList CreateSkiplist()

{

SkipList skiplist=(SkipList *)malloc(sizeof(struct SkipList));

skiplist->level=0;

skiplist->header=CreateNode(MAX_LEVEL-1,0,0);

for(int i=0;i<MAX_LEVEL;i++)

{

skiplist->header->forward[i]=NULL;

}

return skiplist;

}

2 查找

//搜索指定key的value

int Search(SkipList skiplist,int key)

{

Node pre,now=NULL;

pre=skiplist->header;

//从最高层开始搜

int k=skiplist->level;

for(int i=k-1; i >= 0; i--)

{

while((now=pre->forward[i])&&(now->key<=key))

{

if(now->key == key)

{

return now->value;

}

pre=now;

}

}

return NULL;

}

3 插入操作

由于跳表数据结构整体上是有序的，所以在插入时，需要首先查找到合适的位置，然后就是修改指针（和链表中操作类似），然后更新跳表的level变量。

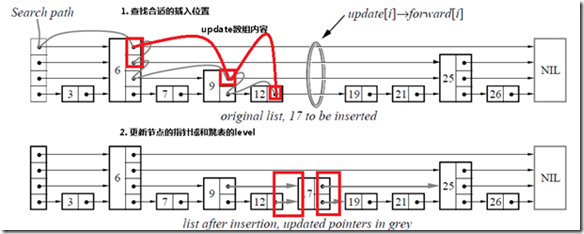
//随机产生层数

int randomLevel()

{

int k=1;

while (rand()%2)

k++;

k=(k<MAX_LEVEL)?k:MAX_LEVEL;

return k;

}

//插入节点

bool Insert(SkipList *skiplist,int key,int value)

{

Node update[MAX_LEVEL];

Node p, q = NULL;

p=skiplist->header;

int k=skiplist->level;

//从最高层往下查找需要插入的位置

//填充update

for(int i=k-1; i >= 0; i--)

{

//q!=NULL

while((q=p->forward[i])&&(q->key<key))

{

p=q;

}

update[i]=p;

}

// 这里已经查找到了合适的位置，并且update数组已经

// 填充好了元素

//不能插入相同的key

if(q&&q->key==key)

{

return false;

}

//产生一个随机层数K

//新建一个待插入节点q

//一层一层插入

k=randomLevel();

// 如果新生成的层数比跳表的层数大的话

// 增加整个跳表的层数

if(k>(skiplist->level))

{

for(int i=skiplist->level; i < k; i++)

{

// 在update数组中将新添加的层指向skiplist->header

update[i] = skiplist->header;

}

skiplist->level=k;

}

q=CreateNode(k,key,value);

//逐层更新节点的指针，和普通列表插入一样

for(int i=0;i<k;i++)

{

q->forward[i]=update[i]->forward[i];

update[i]->forward[i]=q;

}

return true;

}

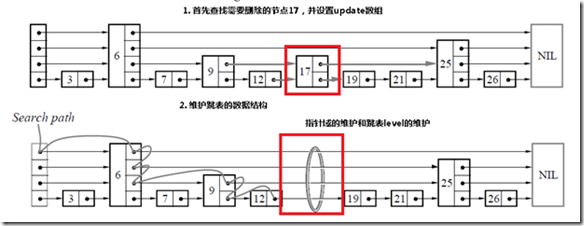
4 删除某个节点

和插入是相同的，首先查找需要删除的节点，如果找到了该节点的话，那么只需要更新指针域，如果跳表的level需要更新的话，进行更新。

//删除指定的key

bool Delete(SkipList skiplist,int key)

{

Node update[MAX_LEVEL];

Node p,q=NULL;

p=skiplist->header;

//从最高层开始搜

int k=skiplist->level;

for(int i=k-1; i >= 0; i--)

{

while((q=p->forward[i])&&(q->key<key))

{

p=q;

}

update[i]=p;

}

if(q&&q->key==key)

{

//逐层删除，和普通列表删除一样

for(int i=0; i<skiplist->level; i++)

{

if(update[i]->forward[i]==q)

{

update[i]->forward[i]=q->forward[i];

}

}

free(q);

//如果删除的是最大层的节点，那么需要重新维护跳表的

for(int i=skiplist->level - 1; i >= 0; i--)

{

if(skiplist->header->forward[i]==NULL)

{

skiplist->level--;

}

}

return true;

}

else

return false;

}

5 参考文献

SkipList论文

ftp://ftp.cs.umd.edu/pub/skipLists/skiplists.pdf

#define MAX_LEVEL 10
typedef struct NodeStructure *Node;

typedef struct NodeStructure
{
	keyType key; // key值
	valueType value; // value值
	// 向前指针数组，根据该节点层数的不同指向不同大小的数组
	NodeStructure *forward[1];
}NodeStructure;

typedef struct SkipList{
	int level;  /* Maximum level of the list
　　	          (1 more than the number of levels in the list) */
	Node header; /* pointer to header */
} * SkipList;

Node CreateNode(int level,int key,int value)
 {
     Node node=(NodeStructure *)malloc(sizeof(NodeStructure)+level*sizeof(NodeStructure*));
     node->key=key;
    node->value=value;
	return node;
}  

SkipList CreateSkiplist()
{
     SkipList skiplist=(SkipList *)malloc(sizeof(struct SkipList));
     skiplist->level=0;
     skiplist->header=CreateNode(MAX_LEVEL-1,0,0);   

	for(int i=0;i<MAX_LEVEL;i++)
	{
        skiplist->header->forward[i]=NULL;
    }
    return skiplist;
 }  

 //搜索指定key的value
int Search(SkipList skiplist,int key)
{
     Node pre,now=NULL;
     pre=skiplist->header;
     //从最高层开始搜
     int k=skiplist->level;
     for(int i=k-1; i >= 0; i--)
	 {
         while((now=pre->forward[i])&&(now->key<=key))
         {
             if(now->key == key)
             {
                 return now->value;
			 }
             pre=now;
         }
     }
     return NULL;
 }  

 //随机产生层数
int randomLevel()
{
    int k=1;
	while (rand()%2)
	k++;
	k=(k<MAX_LEVEL)?k:MAX_LEVEL;
	return k;
 }  

 //插入节点
 bool Insert(SkipList skiplist,int key,int value)
{
     Node update[MAX_LEVEL];
     Node p, q = NULL;
     p=skiplist->header;
    int k=skiplist->level;
	//从最高层往下查找需要插入的位置
     //填充update
     for(int i=k-1; i >= 0; i--)
	 {
		 //q!=NULL
         while((q=p->forward[i])&&(q->key<key))
         {
             p=q;
         }
        update[i]=p;
     }
	 // 这里已经查找到了合适的位置，并且update数组已经
	 // 填充好了元素
     //不能插入相同的key
     if(q&&q->key==key)
    {
         return false;
     }  

     //产生一个随机层数K
    //新建一个待插入节点q
	//一层一层插入
     k=randomLevel();
	// 如果新生成的层数比跳表的层数大的话
	// 增加整个跳表的层数
	if(k>(skiplist->level))
     {
         for(int i=skiplist->level; i < k; i++)
		 {
			// 在update数组中将新添加的层指向skiplist->header
            update[i] = skiplist->header;
         }
         skiplist->level=k;
     }  

    q=CreateNode(k,key,value);
	//逐层更新节点的指针，和普通列表插入一样
     for(int i=0;i<k;i++)
    {
		q->forward[i]=update[i]->forward[i];
        update[i]->forward[i]=q;
     }
     return true;
 }  

 //删除指定的key
bool Delete(SkipList skiplist,int key)
{
    Node update[MAX_LEVEL];
	Node p,q=NULL;
    p=skiplist->header;
    //从最高层开始搜
     int k=skiplist->level;
     for(int i=k-1; i >= 0; i--)
	 {
        while((q=p->forward[i])&&(q->key<key))
         {
             p=q;
         }
         update[i]=p;
     }
     if(q&&q->key==key)
     {
         //逐层删除，和普通列表删除一样
         for(int i=0; i<skiplist->level; i++)
		 {
             if(update[i]->forward[i]==q)
			 {
                update[i]->forward[i]=q->forward[i];
            }
        }
         free(q);
         //如果删除的是最大层的节点，那么需要重新维护跳表的
        for(int i=skiplist->level - 1; i >= 0; i--)
		{
            if(skiplist->header->forward[i]==NULL)
			{
                skiplist->level--;
             }
         }
         return true;
     }
    else
         return false;
 }  

 void Print(SkipList skiplist)
 {
    //从最高层开始打印
     nodeStructure *p,*q=NULL;  

     //从最高层开始搜
     int k=skiplist->level;
	for(int i=k-1; i >= 0; i--)
	{
         p=skiplist->header;
        while(q=p->forward[i])
		{
			printf("%d -> ",p->value);
			p=q;
         }
         printf("\n");
     }
     printf("\n");
 }

 int main()
 {
     SkipList skiplist=CreateSkiplist();
     for(int i=1;i<=19;i++)
     {
         Insert(skiplist,i,i*2);
     }
     Print(skiplist);
     //搜索
     int i=Search(skiplist,4);
     printf("i=%d\n",i);
     //删除
     bool b=Delete(skiplist,4);
     if(b)
         printf("删除成功\n");
     Print(skiplist);
    system("pause");
     return 0;
 }