BestCoder Round #11 题解集合

1001.Alice and Bob

签到题*1，只要x * 2 == n && y * 2 == m就满足条件。

 var
   m, n, x, y : int64;

 begin
   while not eof do begin
     readln(m, n, x, y);
     if (m =  * x) and (n =  * y) then writeln('YES') else writeln('NO');
   end;
 end.

1002.Bob and math problem

我真是WA的不行，但是很明显我的算法没有问题啊。。。

（2014/9/28 22:36更新 原来是Pascal的eof做的死，早知道以后不再也用P了><）

我的算法：统计0到9的个数，然后找出最小的奇数放到末尾，接着从9到0输出，最后输出选出的那个奇数。

中间要判断输出-1的情况：没有奇数；找出一个奇数以后只剩下0了。

 var
   num : array[..] of longint;
   n, ch, i, j, x : longint;

 function find : boolean;
 var
   i : longint;
   flag : boolean;

 begin
   flag := true;
   for i :=  to  do
     if num[i] >  then flag := false;
   find := flag and (n <> );
 end;

 begin
   while not eof do begin
     readln(n);
     if n =  then exit;//这句话没加我就会WA，不知道为啥子捏~
     fillchar(num, sizeof(num), );
     for i :=  to n do begin
       read(x);
       inc(num[x]);
     end;
     ch := ;
     for i :=  to  do begin
       j := i *  - ;
       if num[j] >  then begin
         ch := j;
         dec(num[j]);
         break;
       end;
     end;
     if (ch = ) or find then begin
       writeln(-);
       continue;
     end;
     for i :=  downto  do
       while num[i] >  do begin
         write(i);
         dec(num[i]);
       end;
     writeln(ch);
   end;
 end.

1003.Boring count

这道题看了数据范围就知道要O(n)的算法，因为O(nlogn)的算法有点不大科学。。。

于是我来统计以每个字符s[j]为结尾的满足要求的字符串的个数，不妨设suff[i, j]表示s[i]到s[j]的子串。

又很明显如果suff[i, j]不满足条件了，则suff[i - 1, j]也不满足条件，若令f[j]表示以字符s[j]结尾的最左边满足条件的位置，则f[j]关于j是单调增的。

于是每次枚举j然后查找f[j], ans += j - f[j] +１即可。

 var
   i, x, k, len, left, t1 : longint;
   first, next, num, last : array[..] of longint;
   s : ansistring;
   T : longint;
   ans : int64;

 begin
   readln(T);
   while T >  do begin
     dec(T);
     ans := ;
     readln(s);
     readln(k);
     len := length(s);
     left := ;
     fillchar(first, sizeof(first), );
     fillchar(last, sizeof(last), );
     fillchar(num, sizeof(num), );

     for i :=  to len do begin
       x := ord(s[i]);
       if first[x] =  then first[x] := i;
       inc(num[x]);
       next[last[x]] := i;
       last[x] := i;
       if num[x] > k then begin
         dec(num[x]);
         t1 := first[x];
         first[x] := next[first[x]];
         if t1 > left then left := t1;
       end;
       inc(ans, i - left);
     end;
     writeln(ans);
   end;
 end.

1004.Argestes and Sequence

看我来直播作死：

2014/9/28 22:17　　1004在线BIT交到现在都是MLE，于是我把它删了，发誓明天一定要写出离线算法！

2014/9/28 22:51　　1004在我无数的WA之后终于A掉了！

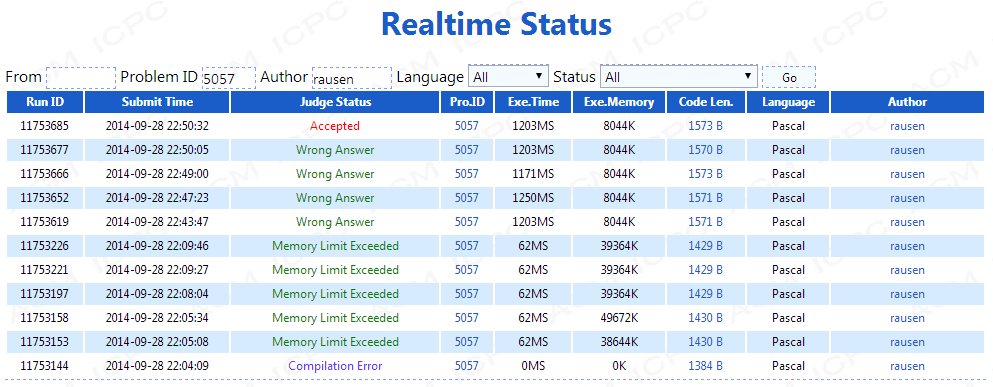
这道题一开始我想到的是线段树，后来发现是求段和于是树状数组（BIT）就可以搞定啦。

但是发现会无限MLE，于是需要一些奇怪的技巧：离线做。

因此我们做10次每次做一位即可。

于是我们现在只考虑某一位上的数如何行统计：

令a[i][j]表示前i个数中j出现的次数。于是操作是单点修改和求前缀和，明显拿BIT维护。

其实还可以分开0到9都做一次，这时候只要700k+(标程)的空间。但是给了3WK的空间就要用满嘛。。。

 var
   ch : char;
   t : longint;
   n, m, i, j, di : longint;
   bit : array[.., ..] of longint;
   opt, l, r, d, p, x, a, b, c, ans : array[..] of longint;

 function lowbit(x : longint) : longint;
 begin
   lowbit := x and (-x);
 end;

 procedure add(x, y, del : longint);
 begin
   while x <= n do begin
     inc(bit[x, y], del);
     inc(x, lowbit(x));
   end;
 end;

 function query(x, y : longint) : longint;
 var
   res : longint;

 begin
   res := ;
   if x <>  then
     while x >  do begin
       inc(res, bit[x, y]);
       dec(x, lowbit(x));
     end;
   query := res;
 end;

 procedure main;
 begin
   readln(n, m);
   for i :=  to n do
     read(a[i]);
   readln;
   for i :=  to m do begin
     read(ch);
     if ch = 'Q' then begin
       opt[i] := ;
       readln(l[i], r[i], d[i], p[i]);
     end else begin
       opt[i] := ;
       readln(x[i], b[i]);
     end;
   end;

   for di :=  to  do begin
     fillchar(bit, sizeof(bit), );
     c := a;
     for i :=  to n do begin
       add(i, a[i] mod , );
       a[i] := a[i] div ;
     end;
     for i :=  to m do begin
       if (opt[i] = ) then begin
         add(x[i], c[x[i]] mod , -);
         add(x[i], b[i] mod , );
         c[x[i]] := b[i];
         b[i] := b[i] div ;
       end else
         if d[i] = di then
           ans[i] := query(r[i], p[i]) - query(l[i] - , p[i]);
     end;
   end;
   for i :=  to m do
     if opt[i] =  then writeln(ans[i]);
 end;

 begin
   readln(t);
   while t >  do begin
     dec(t);
     main;
   end;
 end.