[NOIP2014] 提高组洛谷P1351 联合权值

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu

×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，[b]输出它时要对10007 取余。 [/b]

输入输出样例

输入样例#1：

输出样例#1：

20 74

说明

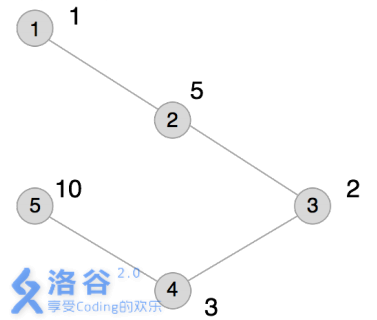
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

选定一个点，找寻与它距离为2的点←无疑太过复杂。

转换思路，选定一个点，找出所有与它相连的点，这些点两两距离都为2

这样问题就简单多了。

依次处理每一个点u，将该点连接的所有点v的权值累加起来，记为s1，点v在统计点u时贡献的权值为(s1-w[v])*w[v] ←乘法原理。

求最大联合权值的思路类似，详见代码。

 #include<iostream>

 #include<cstdio>

 #include<algorithm>

 #include<cmath>

 using namespace std;

 struct Edge{

     int next;

     int to;

     int w;

 }edge[];

 int head[],u,v,ct=;

 int w[];

 long long sum;

 long long mxsum;

 void add_edge(int fr,int t){

     edge[++ct].next=head[fr];

     edge[ct].to=t;

     head[fr]=ct;

     return;

 }

 int sch(int st){//st-第st个点

     int i,j;

     int num=;

     int c[];

     long long s1=;

     int m1=,m2=;

     for(j=head[st];j;j=edge[j].next){

         num++;

         c[num]=w[edge[j].to];

         s1+=c[num];

     }

     for(i=;i<=num;i++){

         sum=(sum+(s1-c[i])*c[i])%;

         if(c[i]>m1){

             m2=m1;m1=c[i];

         }

         else if(c[i]>m2)m2=c[i];

 //        printf("%d: %d %d\n",st,m1,m2);

     }

     if(num)if(m1*m2>mxsum)mxsum=m1*m2;

     if(sum<)sum+=;

     return ;

 }

 int main(){

     int i,j;

     int n;

     scanf("%d",&n);

     for(i=;i<n;i++){

         scanf("%d%d",&u,&v);

         add_edge(u,v);

         add_edge(v,u);

     }

     for(i=;i<=n;i++)scanf("%d",&w[i]);

     for(i=;i<=n;i++){

         sch(i);

         }

     cout<<mxsum<<" "<<sum;

     return ;

 }