洛谷 P2661 信息传递 Label:并查集||强联通分量

题目描述

有n个同学（编号为1到n）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为i的同学的信息传递对象是编号为Ti同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息，但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入输出格式

输入格式：

输入共2行。

第1行包含1个正整数n表示n个人。

第2行包含n个用空格隔开的正整数T1,T2,……,Tn其中第i个整数Ti示编号为i

的同学的信息传递对象是编号为Ti的同学，Ti≤n且Ti≠i

数据保证游戏一定会结束。

输出格式：

输出共 1 行，包含 1 个整数，表示游戏一共可以进行多少轮。

输入输出样例

输入样例#1：

5
2 4 2 3 1

输出样例#1：

3

说明

样例1解释

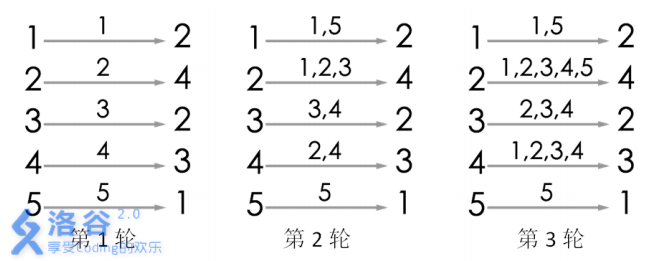
游戏的流程如图所示。当进行完第 3 轮游戏后， 4 号玩家会听到 2 号玩家告诉他自

己的生日，所以答案为 3。当然，第 3 轮游戏后， 2 号玩家、 3 号玩家都能从自己的消息

来源得知自己的生日，同样符合游戏结束的条件。

对于 30%的数据， n ≤ 200；

对于 60%的数据， n ≤ 2500；

对于 100%的数据， n ≤ 200000。

代码

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #define INF 0x3f3f3f3f
 using namespace std;
 vector<int> G[],rG[],vs;
 int N,tot=INF,ans,used[],cmp[],dep[],rank[],pa[];int k=;
 //并查集
 void init_bingchaji(){
     for(int i=;i<=;i++){
         rank[i]=;pa[i]=i;
     }
 }
 int Find(int a){
     if(pa[a]==a) return a;
     else return pa[a]=Find(pa[a]);
 }
 void unite(int a,int b){
     int ta=Find(a),pb=Find(b);
     if(rank[ta]>rank[pb]) pa[pb]=ta;
     else{
         pa[ta]=b;
         if(rank[ta]==rank[pb]) rank[pb]++;
     }
 }

 //强联通分量
 void init_qingliantong(){
     ;
 }
 void add_edge(int a,int b){
     G[a].push_back(b);
     rG[b].push_back(a);
 }
 void dfs(int v){
     used[v]=;
     for(int i=;i<G[v].size();i++){
         if(!used[G[v][i]]) dfs(G[v][i]);
     }
     vs.push_back(v);
 }
 void rdfs(int v,int k,int depth){
     used[v]=;
     dep[v]=depth;
     cmp[v]=k;
     for(int i=;i<rG[v].size();i++){
         if(!used[rG[v][i]]) rdfs(rG[v][i],k,depth+);

         int& now=rG[v][i];
         if(cmp[v]==cmp[now]&&Find(v)==Find(now)){
             for(int j=;j<G[v].size();j++){
 //                printf("v=%d G[v][j]=%d \n",v,G[v][j]);
                 if(Find(now)==Find(G[v][j])){
                     tot=min(tot,dep[G[v][j]]-dep[v]+);
 //                    printf("%d %d\n",v,G[v][j]);
                 }
             }
         }
         else unite(v,rG[v][i]);
     }
     for(int i=;i<rG[v].size();i++){
         if(cmp[v]==cmp[rG[v][i]]) continue;

     }
 }
 void scc(){
     for(int i=;i<=N;i++){
         if(!used[i]) dfs(i);
     }
 //    for(int i=0;i<vs.size();i++) printf("%d ",vs[i]);
     memset(used,,sizeof(used));
     init_bingchaji();
     for(int i=vs.size()-;i>=;i--){
         if(!used[vs[i]]) {
 //            init_bingchaji();
             pa[vs[i]]=vs[i];
             rdfs(vs[i],k++,);
         }
     }
 }

 int main(){
 //    freopen("01.in","r",stdin);
     scanf("%d",&N);
     for(int i=;i<=N;i++){
         int tmp;scanf("%d",&tmp);
         add_edge(i,tmp);
     }
     scc();
 //    for(int i=1;i<=5;i++) printf("%d\n",cmp[i]);
     printf("%d\n",tot);
 }

非常恶心的 强联通

以下为并查集特别版

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<queue>

 using namespace std;

 queue <int>q;
 int n,ans,father[],vis[],ent[];

 int main()
 {
     cin>>n;
     ans=n;
     int x,i,j;
     for(int i=;i<=n;++i)
     {
         scanf("%d",&father[i]);
         ++ent[father[i]];
     }
     for(int i=;i<=n;++i)
     {
         if(ent[i]==)
         {
             q.push(i);
             vis[i]=;
         }
     }
     while(!q.empty())
     {
         x=q.front();
         q.pop();
         --ent[father[x]];
         if(ent[father[x]]==)
         {
             vis[father[x]]=;
             q.push(father[x]);
         }
     }
     for(int i=;i<=n;++i)
     {
         if(ent[i]!=&&vis[i]!=)
         {
             vis[i]=;
             j=father[i];
             x=;
             while(vis[j]==)
             {
                 vis[j]=;
                 j=father[j];
                 ++x;
             }
             if(ans>=x)ans=x;
         }

     }
     printf("%d",ans);
     puts("");
     return ;
 }