《算法设计手册》面试题解答 第五章：图的遍历 附：DFS应用之找挂接点

第五章面试题解答

5-31.

　　DFS和BFS使用了哪些数据结构?

解析：

　　其实刚读完这一章，我一开始想到的是用邻接表来表示图，但其实用邻接矩阵也能实现啊？后来才发现应该回答，BFS用队列实现；DFS可以用栈实现也可以改写成递归形式。用栈来消除递归改写DFS也出现在《算法导论》的练习题22.3-6。

5-32.

　　写一个函数，在遍历二叉查找数的时候，输出第i个结点。

解析：

　　模仿DFS遍历时维护一个进入时间数组和完成时间数组的特点，维护一个全局变量n，在中序遍历的时候，每遍历一个结点就n++，直到n=i时打印这个结点，或者遍历完成时仍然n!=i时报错即可。

题外话：

　　第5章“图遍历”的Interview Problems部分确实只有这两题，而第6章“带权图算法”干脆就没Interview Problems这一部分。其实图本身的表示就比较复杂，几个基本的图算法虽然思路不难，但是代码量不小，同时要写繁琐的初始化方法，写具体算法实现时还要用到各种辅助数据结构，编码起来想少都不行。况且就算真写出来了，正确性的证明又很费功夫（比如拓扑排序、强联通分支），因此面试时除了专门做这个方向的，很少会考到具体的代码书写，更不用说其他变形、改进了。这也就是为什么图相关的面试题并不多的原因。

　　另外提一下，《算法设计手册》上的拓扑排序和强联通分支算法是基于边分类的，而且它把DFS写成了一个可扩充的框架；而《算法导论》则是利用最后完成时间来实现这两个算法，在此之前把DFS写成了一个子程序供这两个算法调用。究竟孰优孰劣我不评价，从先入为主和对我而言易于理解的角度和来说，我更倾向于使用后者。

DFS应用之找挂接点（Articulation Vertices，《算法导论》中文版的翻译）

　　既然提到了《算法设计手册》上DFS的框架写法了，这个算法正好来进行演示。（《算法导论》思考题22-2曾提到了这个概念）。

　　先来看看《算法设计手册》版DFS框架：

//图用邻接表实现
//entry_time[]  某结点开始处理的时间
//exit_time[]    某结点处理完毕的时间
//discoverd[]    某个结点是否已被发现
//process_vertex_early() 某个结点刚发现时采取的处理
//process_edge() 对边的处理
//process_vertex_late() 某个结点所有邻接边处理完后的动作
//以上三个函数决定了DFS的行为，如果只需要基本的功能，可以实现为空操作，或者输出该结点/边用于追踪遍历过程

dfs(graph *g, int v)
{
    edgenode *p; /* temporary pointer */
    int y; /* successor vertex */
    if (finished) return; /* allow for search termination */

    discovered[v] = TRUE;
    time = time + ;
    entry_time[v] = time;
    process_vertex_early(v);
    p = g->edges[v];
    while (p != NULL) {
          y= p->y;
          if (discovered[y] == FALSE) {
               parent[y] = v;
               process_edge(v,y);
               dfs(g,y);
          }
          else if ((!processed[y]) || (g->directed))
               process_edge(v,y);
           if (finished) return;
               p = p->next;
     }
     process_vertex_late(v);
     time = time + ;
     exit_time[v] = time;
     processed[v] = TRUE;
}    

《算法设计手册》版DFS框架

　　挂接点是指，如果我们从连通图中删除这个结点，会导致图不再连通。下图中的白点就是挂接点，可以把它看作为图上最脆弱的点。

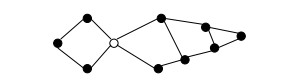
　　使用DFS或BFS写一个暴力算法很简单：删除一个结点，用DFS或BFS判断是否连通；恢复原图，删除下一个结点继续判断，直至所有接点都判断过。如果结点数n个，边数m个，暴力算法时间复杂度为O(n(m+n))。

　　现在用DFS遍历时生成树的角度来看。对于这棵树上所有在原图的边，归为TREE边；其余所有边是BACK边，即它们指向一个先于这个结点遍历的另一个结点。

　　可以发现一些规律：

DFS树的叶结点不可能是挂接点，删去它树的连通性未被破坏。只有树的内结点可能是挂接点。

对于DFS树的根，如果它只有一个孩子，那么删去它和删去一个叶结点是一样的。而孩子多于1个时，删去根会导致孩子们不再连通，也即它是挂接点。

对于一个BACK边，它连接的两个结点的TREE路径（即DFS时形成的路径）上的所有结点都不可能是挂接点。

　　寻找挂接点需要维护BACK边连接DFS树上结点与其祖先的信息。用reachable_ancesor[v]表示结点v用BACK边能连接的最老祖先（初始化为v），tree_out_degree[v]表示结点在DFS树的出度。edge_classification(int x,int y)用于判断(x,y)是TREE还是BACK。

int reachable_ancestor[MAXV+]; /* earliest reachable ancestor of v */
int tree_out_degree[MAXV+]; /* DFS tree outdegree of v */
process_vertex_early(int v)
{
    reachable_ancestor[v] = v;
}

process_edge(int x, int y)
{
    int class; /* edge class */
    class = edge_classification(x,y);
    if (class == TREE)
        tree_out_degree[x] = tree_out_degree[x] + ;
    if ((class == BACK) && (parent[x] != y)) {
        if (entry_time[y] < entry_time[ reachable_ancestor[x] ] )
            reachable_ancestor[x] = y;
    }
}

int edge_classification(int x, int y)
{
    if (parent[y] == x)
        return TREE;
    else
        return BACK;
}

　　下面是v与祖先的连通性和v是否是挂接点的关系，一共是三种情况：

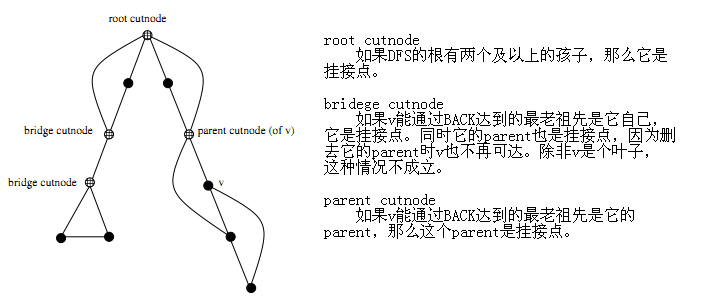
　　用代码实现在process_vertex_late()里，即：

process_vertex_late(int v)
{
    bool root; /* is the vertex the root of the DFS tree? */
    int time_v; /* earliest reachable time for v */
    int time_parent; /* earliest reachable time for parent[v] */
    if (parent[v] < ) { /* test if v is the root */
        if (tree_out_degree[v] > )
            printf("root articulation vertex: %d \n",v);
        return;
    }

    root = (parent[parent[v]] < ); /* is parent[v] the root? */
    if ((reachable_ancestor[v] == parent[v]) && (!root))
        printf("parent articulation vertex: %d \n",parent[v]);

    if (reachable_ancestor[v] == v) {
        printf("bridge articulation vertex: %d \n",parent[v]);
        if (tree_out_degree[v] > ) /* test if v is not a leaf */
            printf("bridge articulation vertex: %d \n",v);
    }

    time_v = entry_time[reachable_ancestor[v]];
    time_parent = entry_time[ reachable_ancestor[parent[v]] ];
    if (time_v < time_parent)
        reachable_ancestor[parent[v]] = reachable_ancestor[v];
}

　　最后几行用entry_time[v]表示v的年龄，time_v是v通过BACK边达到的最老结点。如果v的parent能通过v的BACK到达v的最老祖先，那么parent(v)肯定不是挂接点，下次处理parent(v)时做出这样的标记让它能通过v的BACK到达v的最老祖先。